Интернет магазин китайских планшетных компьютеров |
||
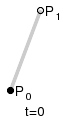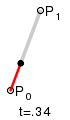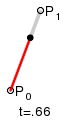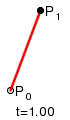
Компьютеры - Кривая Безье - Построение кривых Безье23 января 2011Оглавление: 1. Кривая Безье 2. Определение 3. Построение кривых Безье 4. Применение в компьютерной графике 5. Преобразование квадратичных кривых Безье в кубические Линейные кривыеПараметр t в функции, описывающей линейный случай кривой Безье, определяет где именно на расстоянии от P0 до P1 находится B. Например, при t = 0,25 значение функции B соответствует четверти расстояния между точками P0 и P1. Параметр t изменяется от 0 до 1, а B описывает отрезок прямой между точками P0 и P1.
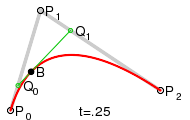
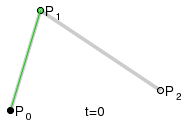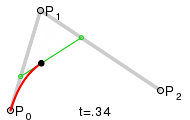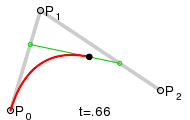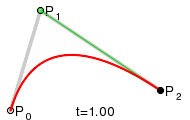
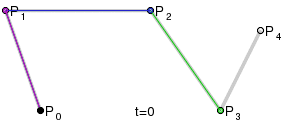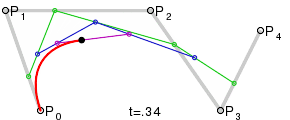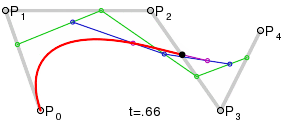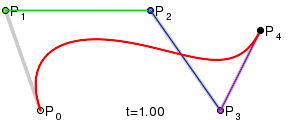
Квадратичные кривыеДля построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q0 и Q1 из условия чтобы параметр t изменялся от 0 до 1:
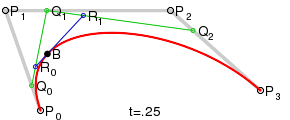
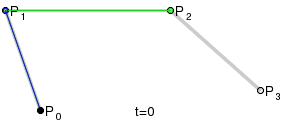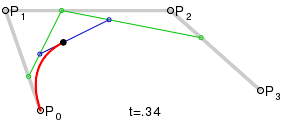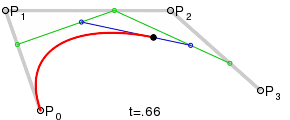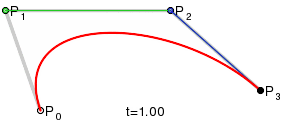
Кривые высших степенейДля построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки Q0, Q1 и Q2, описывающие линейные кривые, а также точки R0 и R1, которые описывают квадратичные кривые: более простое уравнение p0q0/p0q1=q1p1/p1p2=bq0/q1q0
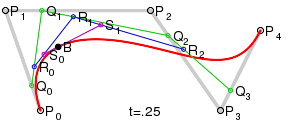
Для кривых четвёртой степени это будут точки Q0, Q1, Q2 и Q3, описывающие линейные кривые, R0, R1 и R2, которые описывают квадратичные кривые, а также точки S0 и S1, описывающие кубические кривые Безье:
Свойства кривой Безье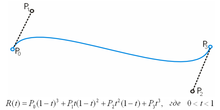
Просмотров: 8697
|