Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Кривая Безье - Определение23 января 2011Оглавление: 1. Кривая Безье 2. Определение 3. Построение кривых Безье 4. Применение в компьютерной графике 5. Преобразование квадратичных кривых Безье в кубические Кривая Безье — параметрическая кривая, задаваемая выражением где
где Виды кривых БезьеЛинейные кривыеПри n = 1 кривая представляет собой отрезок прямой линии, опорные точки P0 и P1 определяют его начало и конец. Кривая задаётся уравнением:
Квадратичные кривыеКвадратичная кривая Безье задаётся 3-мя опорными точками: P0, P1 и P2.
Квадратичные кривые Безье в составе сплайнов используются для описания формы символов в шрифтах TrueType и в SWF файлах. Кубические кривыеВ параметрической форме кубическая кривая Безье описывается следующим уравнением:
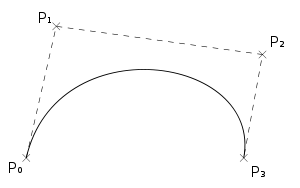
Кубическая кривая Безье
Четыре опорные точки P0, P1, P2 и P3, заданные в 2-х или 3-мерном пространстве определяют форму кривой. Линия берёт начало из точки P0 направляясь к P1 и заканчивается в точке P3 подходя к ней со стороны P2. То есть кривая не проходит через точки P1 и P2, они используются для указания её направления. Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P3. В матричной форме кубическая кривая Безье записывается следующим образом:
где В современных графических системах, таких как PostScript, Metafont и GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых. Просмотров: 8697
|
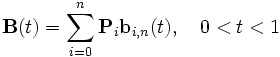
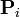 — функция компонент векторов опорных вершин, а
— функция компонент векторов опорных вершин, а 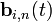 — базисные функции кривой Безье, называемые также полиномами Бернштейна.
— базисные функции кривой Безье, называемые также полиномами Бернштейна.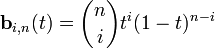 ,
,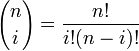 — число сочетаний из n по i, где n — степень полинома, i — порядковый номер опорной вершины.
— число сочетаний из n по i, где n — степень полинома, i — порядковый номер опорной вершины.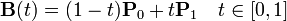 .
.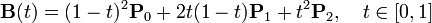 .
.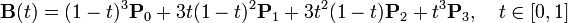 .
.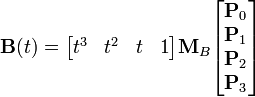 ,
,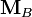 называется базисной матрицей Безье:
называется базисной матрицей Безье: