Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Криптоанализ RSA29 мая 2011Оглавление: 1. Криптоанализ RSA 2. Элементарные атаки 3. Малые значения секретной экспоненты Данная статья описывает условия использования криптоалгоритма с открытым ключом RSA, упрощающие криптоаналитические атаки, и методы исключения таких условий. ВведениеНа 2009 год система шифрования на основе RSA считается надёжной, начиная с размера Группе учёных из Швейцарии, Японии, Франции, Нидерландов, Германии и США удалось успешно вычислить данные, зашифрованные при помощи криптографического ключа стандарта RSA длиной 768 бит. По словам исследователей, после их работы в качестве надежной системы шифрования можно рассматривать только RSA-ключи длиной 1024 бита и более. Причём от шифрования ключом длиной в 1024 бит стоит отказаться в ближайшие три-четыре года. Как следует из описания работы, вычисление значений ключа осуществлялось общим методом решета числового поля. На первый шаг было потрачено около полугода вычислений на 80 процессорах, что составило около 3 % времени, потраченного на главный этап алгоритма, который выполнялся на сотнях компьютеров в течение почти двух лет. Если интерполировать это время на работу одного процессора AMD Opteron 2.2ГГц с 2Гб памяти, то получилось бы порядка 1500 лет. Обработка данных после просеивания для следующего ресурсоёмкого шага потребовалось несколько недель на малом количестве процессоров. Заключительный шаг после нахождения нетривиальных решений ОСЛУ занял не более 12 часов. Решение ОСЛУ проводилось с помощью метода Видемана на нескольких раздельных кластерах и длилось чуть менее 4 месяцев. При этом размер разреженной матрицы составил 192 796 550х192 795 550 при наличии 27 795 115 920 ненулевых элементов. Для хранения матрицы на жёстком диске понадобилось около 105 гигабайт. В то же время понадобилось около 5 терабайт сжатых данных для построения данной матрицы. В итоге группе удалось вычислить 232-цифровой ключ, открывающий доступ к зашифрованным данным. Исследователи уверены, что используя их метод факторизации, взломать 1024-битный RSA-ключ будет возможно в течение следующей декады. Зная разложение модуля
не позволяет разложить большое целое за приемлемое время. Будем рассматривать возможные атаки на RSA, которые позволяют взломать эту систему, не используя прямого разложения модуля n на произведение двух простых чисел. Просмотров: 3869
|
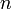 в 1024 бита.
в 1024 бита.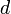 и тем самым взломать RSA. Однако на сегодняшний день самый быстрый алгоритм факторизации — решето обобщённого числового поля, скорость которого для k-битного целого числа составляет
и тем самым взломать RSA. Однако на сегодняшний день самый быстрый алгоритм факторизации — решето обобщённого числового поля, скорость которого для k-битного целого числа составляет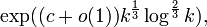 для некоторого
для некоторого 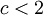 ,
,