|
|
|
Компьютеры - Кластерный анализ - Формальная постановка задачи кластеризации23 января 2011
Оглавление:
1. Кластерный анализ
2. Задачи и условия
3. Анализ и интерпретация его результатов
4. Типология задач кластеризации
5. Формальная постановка задачи кластеризации
6. Применение
Пусть 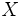 — множество объектов, — множество объектов, 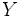 — множество номеров кластеров. Задана функция расстояния между объектами — множество номеров кластеров. Задана функция расстояния между объектами 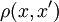 . Имеется конечная обучающая выборка объектов . Имеется конечная обучающая выборка объектов 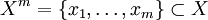 . Требуется разбить выборку на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике . Требуется разбить выборку на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике 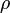 , а объекты разных кластеров существенно отличались. При этом каждому объекту , а объекты разных кластеров существенно отличались. При этом каждому объекту  приписывается номер кластера приписывается номер кластера 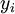 . .
Алгоритм кластеризации — это функция 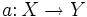 , которая любому объекту , которая любому объекту 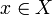 ставит в соответствие номер кластера ставит в соответствие номер кластера 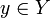 . Множество . Множество 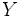 в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации. в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации.
Кластеризация отличается от классификации тем, что метки исходных объектов 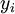 изначально не заданы, и даже может быть неизвестно само множество изначально не заданы, и даже может быть неизвестно само множество 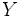 . .
Решение задачи кластеризации принципиально неоднозначно, и тому есть несколько причин:
- не существует однозначно наилучшего критерия качества кластеризации. Известен целый ряд эвристических критериев, а также ряд алгоритмов, не имеющих чётко выраженного критерия, но осуществляющих достаточно разумную кластеризацию «по построению». Все они могут давать разные результаты.
- число кластеров, как правило, неизвестно заранее и устанавливается в соответствии с некоторым субъективным критерием.
- результат кластеризации существенно зависит от метрики, выбор которой, как правило, также субъективен и определяется экспертом.
Просмотров: 8243
|
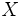 — множество объектов,
— множество объектов, 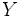 — множество номеров кластеров. Задана функция расстояния между объектами
— множество номеров кластеров. Задана функция расстояния между объектами 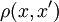 . Имеется конечная обучающая выборка объектов
. Имеется конечная обучающая выборка объектов 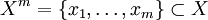 . Требуется разбить выборку на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике
. Требуется разбить выборку на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике 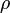 , а объекты разных кластеров существенно отличались. При этом каждому объекту
, а объекты разных кластеров существенно отличались. При этом каждому объекту  приписывается номер кластера
приписывается номер кластера 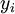 .
.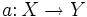 , которая любому объекту
, которая любому объекту 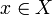 ставит в соответствие номер кластера
ставит в соответствие номер кластера 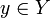 . Множество
. Множество