Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Классификация документов - Обучающие методы23 января 2011Оглавление: 1. Классификация документов 2. Постановка задачи 3. Обучающие методы 4. Применение Наивная байесовская модельНаивная байесовская модель является вероятностным методом обучения. Вероятность того, что документ d попадёт в класс c записывается как P. Поскольку цель классификации - найти самый подходящий класс для данного документа, то в наивной байесовской классификации задача состоит в нахождении наиболее вероятного класса cm
Вычислить значение этой вероятности напрямую невозможно, поскольку для этого нужно, чтобы обучающее множество содержало все возможные комбинации классов и документов. Однако, используя формулу Байеса, можно переписать выражение для P
где знаменатель P опущен, так как не зависит от c и, следовательно, не влияет на нахождение максимума; P - вероятность того, что встретится класс c, независимо от рассматриваемого документа; P - вероятность встретить документ d среди документов класса c. Используя обучающее множество, вероятность P можно оценить как
где Nc - количество документов в классе c, N - общее количество документов в обучающем множестве. Здесь использован другой знак для вероятности, поскольку с помощью обучающего множества можно лишь оценить вероятность, но не найти её точное значение. Чтобы оценить вероятность
Оценка вероятнотей P с помощью обучающего множества будет
где Tct - количество вхождений терма t во всех документах класса c; Tc - общее количество термов в документах класса c. При подсчёте учитываются все повторные вхождения. После того, как классификатор "обучен", то есть найдены величины
Чтобы избежать в последней формуле переполнения снизу из-за большого числа сомножителей, на практике вместо произведения обычно используют сумму логарифмов. Логарифмирование не влияет на нахождение максимума, так как логирфм является монотонно возрастающей функцией. Поэтому в большинстве реализаций вместо последней формулы используется
Эта формула имеет простую интерпретацию. Шансы классифицировать документ часто встречающимся классом выше, и слагаемое Просмотров: 4112
|
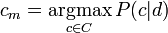
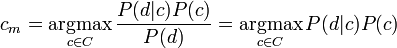
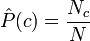
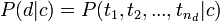 , где tk - терм из документа d, nd - общее количество термов в документе, необходимо ввести упрощающие предположения о условной независимости термов и о независимости позиций термов. Другими словами, мы пренебрегаем, во-первых, тем фактом, что в тексте на естественном языке появление одного слова часто тесно связано с появлением других слов, и, во-вторых, что вероятность встретить одно и то же слово различна для разных позиций в тексте. Именно из-за этих грубых упрощений рассматриваемая модель естественного языка называется наивной. Итак, в свете сделанных предположений, используя правило умножения вероятностей независимых событий, можно записать
, где tk - терм из документа d, nd - общее количество термов в документе, необходимо ввести упрощающие предположения о условной независимости термов и о независимости позиций термов. Другими словами, мы пренебрегаем, во-первых, тем фактом, что в тексте на естественном языке появление одного слова часто тесно связано с появлением других слов, и, во-вторых, что вероятность встретить одно и то же слово различна для разных позиций в тексте. Именно из-за этих грубых упрощений рассматриваемая модель естественного языка называется наивной. Итак, в свете сделанных предположений, используя правило умножения вероятностей независимых событий, можно записать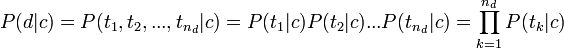
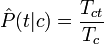
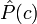 и
и 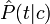 , можно отыскать класс документа
, можно отыскать класс документа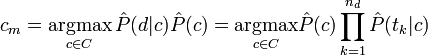
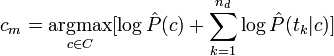
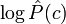 вносит в общую сумму соответствующий вклад. Величины же
вносит в общую сумму соответствующий вклад. Величины же 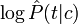 тем больше, чем важнее терм t для идентификации класса c, и, соответственно, тем весомее их вклад в общую сумму.
тем больше, чем важнее терм t для идентификации класса c, и, соответственно, тем весомее их вклад в общую сумму.