Интернет магазин китайских планшетных компьютеров |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Компьютеры - Индекс совпадений23 января 2011Оглавление: 1. Индекс совпадений 2. Пример использования Индекс совпадений - один из методов криптоанализа шифра Виженера. Описание метода опубликовано Уильямом Фридманом в 1922 году. ПредпосылкиВзлом шифра Виженера состоит из двух этапов — определение длины ключевого слова и использование частотного анализа для взлома нескольких шифров Цезаря. C 1863 года можно было использовать метод Касиски, однако этот метод предполагал достаточно длительный ручной поиск совпадающих подстрок, которые также могут иметь низкую вероятность появления в шифротексте. Новый метод, описанный Фридманом в 1922 году, предлагал более быстрый и простой способ определения длины ключа. Описание методаИндекс совпаденийРассмотрим текст, написанный на некотором языке. Алфавит данного языка будем полагать состоящим из m букв. Рассмотрим достаточно длинную строку откуда при достаточно больших n и определении pi как pi = fi / n получаем приближённую формулу: Теперь, если предположить, что наш текст написан на естественном языке, является достаточно длинным и его характеристики соответствуют известным нам характеристикам данного языка, то для него можно получить ожидаемый индекс совпадений:
Для работы метода индекса совпадений важно, что данная характеристика не меняется, если текст на языке зашифрован с использованием моноалфавитного шифра, такого, как шифр Цезаря. Для случайной строки символов алфавита это значение примерно равно то есть 0,03125 для русского языка и 0,03856 для английского языка. Важным свойством является то, что индекс совпадения для строки не меняется при шифровании этой строки моноалфавитным шифром. Взаимный индекс совпаденийТеперь рассмотрим две строки Пусть fi,gi - количество i-ой буквы алфавита в первой и второй строке соответственно. Тогда взаимный индекс совпадений будет равен: Достаточно легко показать следующие свойства:
Взаимный индекса совпадений для зашифрованных строкПусть Правая часть выражения зависит только от величины ki − kj, которая называется относительным сдвигом строк мы можем построить таблицу относительных сдвигов для любого α от 1 до m / 2, используя их для нахождения значений и в случае m / 2 < α < m.
Стоит отметить, что хотя значения для ненулевых сдвигов что для русского, что для английского языка различаются между собой не очень сильно, они достаточно хорошо отличаются от значения индекса при нулевом сдвиге. Метод индекса совпаденийВозьмём строку Просмотров: 4840
|
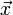 из n букв. Если fi задаёт количество i-той буквы алфавита в строке
из n букв. Если fi задаёт количество i-той буквы алфавита в строке 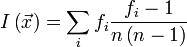
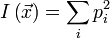
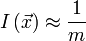
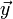 с длинами n и n' соответственно, составленные из букв некоторого алфавита. Алфавит также имеет m букв. Взаимным индексом совпадений этих строк будет называть вероятность того, что буква, случайно выбранная из первой строки, совпадёт со случайно выбранной буквой второй строки.
с длинами n и n' соответственно, составленные из букв некоторого алфавита. Алфавит также имеет m букв. Взаимным индексом совпадений этих строк будет называть вероятность того, что буква, случайно выбранная из первой строки, совпадёт со случайно выбранной буквой второй строки.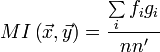
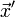 , с такими же частотами символов
, с такими же частотами символов 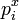 , как и в исходной строке, то её взаимный индекс со второй строкой
, как и в исходной строке, то её взаимный индекс со второй строкой 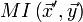 будет примерно равен взаимному индексу оригинальной строки и второй строки
будет примерно равен взаимному индексу оригинальной строки и второй строки 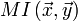
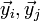 — строки, зашифрованные шифром Виженера с ключевым словом
— строки, зашифрованные шифром Виженера с ключевым словом 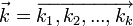 . Можно показать, что для этих строк величина индекса совпадений примерно равна:
. Можно показать, что для этих строк величина индекса совпадений примерно равна: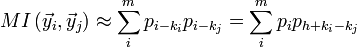
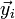 и
и 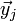 . С учётом очевидного равенства
. С учётом очевидного равенства