Компьютеры - Графический метод решения задачи линейного программирования22 января 2011
Область применения.
Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно.
Пусть задача линейного программирования задана в двумерном пространстве, то есть ограничения содержат две переменные. Найти минимальное значение функции
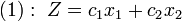
при
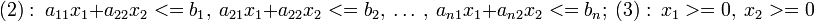
Допустим, что система при условии совместна и её многоугольник решений ограничен. Каждое из неравенств и, как отмечалось выше, определяет полуплоскость с граничными прямыми: 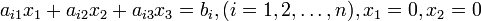 . Линейная функция при фиксированных значениях . Линейная функция при фиксированных значениях 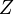 является уравнением прямой линии: является уравнением прямой линии: 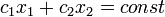 . Построим многоугольник решений системы ограничений и график линейной функции при . Построим многоугольник решений системы ограничений и график линейной функции при 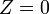 . Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию. Найти точку многоугольника решений, в которой прямая . Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию. Найти точку многоугольника решений, в которой прямая 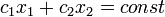 опорная и функция опорная и функция 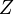 при этом достигает минимума. при этом достигает минимума.
Значения 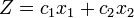 возрастают в направлении вектора возрастают в направлении вектора 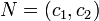 , поэтому прямую , поэтому прямую 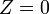 передвигаем параллельно самой себе в направлении вектора передвигаем параллельно самой себе в направлении вектора 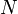 . Прямая дважды становится опорной по отношению к многоугольнику решений, причем минимальное значение принимает в точке . Прямая дважды становится опорной по отношению к многоугольнику решений, причем минимальное значение принимает в точке 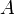 . Координаты точки . Координаты точки 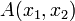 находим, решая систему уравнений прямых находим, решая систему уравнений прямых 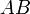 и и 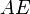 . .
Если многоугольник решений представляет собой неограниченную многоугольную область, то возможны два случая.
Случай 1. Прямая 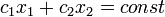 , передвигаясь в направлении вектора , передвигаясь в направлении вектора 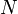 или противоположно ему, постоянно пересекает многоугольник решений и ни в какой точке не является опорной к нему. В этом случае линейная функция не ограничена на многоугольнике решений как сверху, так и снизу. или противоположно ему, постоянно пересекает многоугольник решений и ни в какой точке не является опорной к нему. В этом случае линейная функция не ограничена на многоугольнике решений как сверху, так и снизу.
Случай 2. Прямая, передвигаясь, всё же становится опорной относительно многоугольника решений. Тогда в зависимости от вида области линейная функция может быть ограниченной сверху и неограниченной снизу, ограниченной снизу и неограниченной сверху, либо ограниченной как снизу, так и сверху.
Просмотров: 1748
|
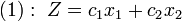
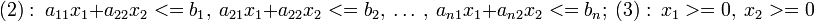
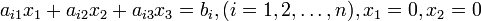 . Линейная функция при фиксированных значениях
. Линейная функция при фиксированных значениях 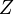 является уравнением прямой линии:
является уравнением прямой линии: 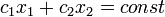 . Построим многоугольник решений системы ограничений и график линейной функции при
. Построим многоугольник решений системы ограничений и график линейной функции при 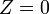 . Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию. Найти точку многоугольника решений, в которой прямая
. Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию. Найти точку многоугольника решений, в которой прямая 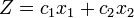 возрастают в направлении вектора
возрастают в направлении вектора 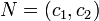 , поэтому прямую
, поэтому прямую 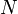 . Прямая дважды становится опорной по отношению к многоугольнику решений, причем минимальное значение принимает в точке
. Прямая дважды становится опорной по отношению к многоугольнику решений, причем минимальное значение принимает в точке 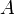 . Координаты точки
. Координаты точки 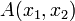 находим, решая систему уравнений прямых
находим, решая систему уравнений прямых 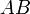 и
и 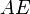 .
.