Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Формальная система - Свойства дедуктивных теорий23 января 2011Оглавление: 1. Формальная система 2. Определение и разновидности 3. Свойства дедуктивных теорий 4. Важнейшие выводы ПротиворечивостьТеория, в которой множество теорем покрывает всё множество формул, называется противоречивой. В противном случае теория называется непротиворечивой. Выяснение противоречивости теории — одна из важнейших и иногда сложнейших задач формальной логики. После выяснения противоречивости теория, как правило, не имеет дальнейшего ни теоретического, ни практического применения. ПолнотаТеория называется полной, если в ней для любой формулы F выводима либо сама F, либо ее отрицание Независимость аксиомОтдельная аксиома теории считается независимой, если эту аксиому нельзя вывести из остальных аксиом. Зависимая аксиома по сути избыточна, и ее удаление из системы аксиом никак не отразится на теории. Вся система аксиом теории называется независимой, если каждая аксиома в ней независима. РазрешимостьТеория называется разрешимой, если в ней понятие теоремы эффективно, то есть существует эффективный процесс, позволяющий для любой формулы за конечное число шагов определить, является она теоремой или нет. Просмотров: 3324
|
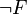 . В противном случае, теория содержит недоказуемые утверждения, и называется неполной.
. В противном случае, теория содержит недоказуемые утверждения, и называется неполной.