Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Фибоначчиева система счисления - Обобщение на вещественные числа22 января 2011Оглавление: 1. Фибоначчиева система счисления 2. Обобщение на вещественные числа 3. Фибоначчиево умножение
Похожее устройство имеет позиционная система счисления с иррациональным основанием, равным золотому сечению Любое вещественное число x из отрезка допускает разложение в ряд через отрицательные степени золотого сечения: где {εk} обладает тем же свойством отсутствия соседних единиц. Коэффициенты находятся последовательным сравнением x с где N таково, что Эти формулы полностью аналогичны формулам для обычных позиционных систем с целыми основаниями. Оказывается, что любое неотрицательное целое число имеет представление лишь с конечным количеством единиц, то есть в виде конечной суммы неповторяющихся степеней золотого сечения. Аналогия между числами Фибоначчи и степенями золотого сечения основана на одинаковой форме тождеств: позволяющих устранение соседних единиц. Прямой связи между представлением натуральных чисел в системе золотого сечения и в фибоначчиевой не имеется. Правила сложения аналогичны показанным выше с той поправкой, что перенос в сторону младших разрядов распространяется без ограничения. В данной системе счисления можно производить и умножение. Просмотров: 6547
|
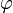
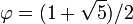 .
.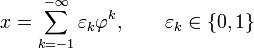
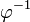 — золотым сечением отрезка, вычитанием
— золотым сечением отрезка, вычитанием 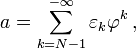
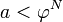 . Разумеется, следует считать что
. Разумеется, следует считать что 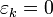 для всех
для всех 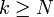 .
.