Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Эллиптическая криптография - Реализация шифрования22 января 2011Оглавление: 1. Эллиптическая криптография 2. Эллиптические кривые над конечными полями 3. Теорема Хассе 4. Реализация шифрования 5. Приложения Конкретные реализации алгоритмов шифрования на эллиптической кривой описаны выше. Здесь мы рассмотрим общие принципы эллиптической криптографии. Набор параметровДля использования эллиптической криптографии все участники должны согласовать все параметры, определяющие эллиптическую кривую, т.е. набор параметров криптографического протокола. Эллиптическая кривая определяется константами a и b из уравнения. Абелева подгруппа точек является циклической и задается одной порождающей точкой G. При этом кофактор Итак, для поля характеристики 2 набор параметров: , а для конечного поля Существует несколько рекомендованных наборов параметров:
Для создания собственного набора параметров необходимо:
Для нахождения кривой для заданного набора параметров используются два метода:
Существует несколько классов криптографически «слабых» кривых, которых следует избегать:
Быстрая редукцияДеление по модулю p могут выполняться быстрее, если в качестве p выбрать простое число близкое к степени числа 2. В частности, в роли p может выступать простое число Мерсенна. Например, хорошим выбором являются p = 2 − 1 или p = 2 − 2 − 2 − 2 − 2 − 2 − 2 − 1. Национальный институт стандартов и технологий рекомендует использовать подобные простые числа в качестве p. Ещё одним преимуществом кривых, рекомендованных NIST, является выбор значения a = − 3, что ускоряет операцию сложения в координатах Якоби. Эллиптические кривые, рекомендованные NISTNIST рекомендует 15 эллиптических кривых. В частности, FIPS 186-3 рекомендует 10 конечных полей. Некоторые из них:
Причем для каждого конечного поля рекомендуется одна эллиптическая кривая. Эти конечные поля и эллиптические кривые выбраны из-за высокого уровня безопасности и эффективности программной реализации. Размер ключаСамым быстрым алгоритмам, решающим задачу дискретного логарифмирования на эллиптических кривых, таким как алгоритм Шенкса и ρ-метод Полларда, необходимо Самые сложные схемы на эллиптических кривых, публично взломанные к настоящему времени, содержали 112-битный ключ для конечного простого поля и 109-битный ключ для конечного поля характеристики 2. В июле 2009 года, кластер из более чем 200 Sony Playstation 3 за 3.5 месяца нашел 109-битный ключ. Ключ над полем характеристики 2 был найден в апреле 2004 года, с использованием 2600 компьютеров, в течение 17 месяцев. Просмотров: 8660
|
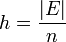 , где n — порядок точки G, должен быть небольшим.
, где n — порядок точки G, должен быть небольшим.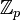 , где p > 3, набор параметров: .
, где p > 3, набор параметров: .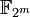 , где m - не простое число. Шифрование на этих кривых подвержено атакам Вейля.
, где m - не простое число. Шифрование на этих кривых подвержено атакам Вейля.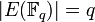 уязвимы для атаки, которая отображает точки данной кривой в аддитивную группу поля
уязвимы для атаки, которая отображает точки данной кривой в аддитивную группу поля 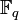 .
.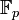 , где простое p имеет длину 192, 224, 256, 384 или 521 битов.
, где простое p имеет длину 192, 224, 256, 384 или 521 битов.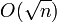 операций. Поэтому размер поля должен как минимум в два раза превосходить размер ключа. Например, для 128-битного ключа рекомендуется использовать эллиптическую кривую над полем
операций. Поэтому размер поля должен как минимум в два раза превосходить размер ключа. Например, для 128-битного ключа рекомендуется использовать эллиптическую кривую над полем