Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Эллиптическая криптография - Эллиптические кривые над конечными полями22 января 2011Оглавление: 1. Эллиптическая криптография 2. Эллиптические кривые над конечными полями 3. Теорема Хассе 4. Реализация шифрования 5. Приложения Эллиптической кривой называется множество точек , удовлетворяющих уравнению:
Это уравнение может рассматриваться над произвольными полями и, в частности, над конечными полями, представляющими для криптографии особый интерес. В криптографии эллиптические кривые рассматриваются над двумя типами конечных полей: простыми полями нечётной характеристики и полями характеристики 2). Эллиптические кривые над полями нечётной характеристикиНад полем где Группой точек эллиптической кривой E над полем Следует отметить, что в ПримерРассмотрим эллиптическую кривую y = x + 3x + 2 над полем Просмотров: 8682
|
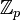 характеристики p > 3 уравнение эллиптической кривой E можно привести к виду:
характеристики p > 3 уравнение эллиптической кривой E можно привести к виду: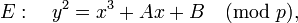
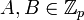 — константы, удовлетворяющие
— константы, удовлетворяющие 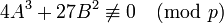 .
. :
: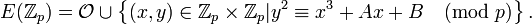
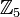 . На этой кривой в частности лежит точка , так как
. На этой кривой в частности лежит точка , так как 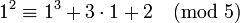 .
.