|
|
|
Компьютеры - ECDSA - ECDSA согласно стандарту ANSI X9.6229 мая 2011
Оглавление:
1. ECDSA
2. Выбор параметров
3. ECDSA согласно стандарту ANSI X9.62
4. Преимущества ECDSA над DSA
5. Практическая реализация
Для практического применения алгоритма ECDSA налагают ограничения на поля, в которых определены эллиптические кривые. Более того для избежания некоторых известных атак, ограничения накладываются и на уравнения, задающие эллиптические кривые, и на порядок базовых точек. Для простоты в данном разделе будем рассматривать только конечные Fp.
Требования к эллиптической кривой
Для того, чтобы избежать известных атак, основанных на проблеме дискретного логарифма в группе точек эллиптической кривой, необходимо, чтобы число точек эллиптической кривой E делилось на достаточно большое простое число n. Стандарт ANSI X9.62 требует n > 2. Уравнение эллиптической кривой строится специфическим образом, используя случайные/псевдослучайные коэффициенты.
Главными параметрами при построении эллиптической кривой являются:
- размерность поля p, где p явлется простым числом;
- два элемента поля Fp — a и b, определенные уравнением эллиптической кривой E, где E имеет вид:
-
y = x + ax + b,
- где a, b \in Fp, и 4a + 27b \not\equiv 0 .
- два элемента поля Fp — xG и yG, которые определяют конечную точку G = — генератор группы E
- порядок q точки G, где q > 2 и q > 4
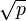
- сомножитель h = #E/q, где обозначение #E означает порядок группы точек эллиптической кривой E.
Генерация главных параметров
Один из способом генерирования криптографически надежных параметров заключается в следующем:
- Выбираем коэффициенты a и b специфическим образом используя в вычислениях случайные/псевдослучайные числа. Пусть E — эллиптическая кривая — y = x + ax + b;
- Вычисляем
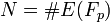 ; ;
- Проверяем, что N имеет делитель, который является большим простым числом q" src="http://upload.wikimedia.org/math/2/f/8/2f88ff4ba5c3fc28d9e0bbadd4ae73fe.png" />. Если нет, то нужно вернуться на шаг 1.
- Проверяем, что q не делит p − 1 для каждого k,
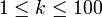 . Если нет, то нужно вернуться на шаг 1; . Если нет, то нужно вернуться на шаг 1;
- Проверяем, что
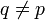 . Если нет, то нужно вернуть на шаг 1; . Если нет, то нужно вернуть на шаг 1;
- Берем случайную точку
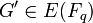 и положить G =G'. Повторяем до тех пор пока и положить G =G'. Повторяем до тех пор пока 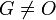 . .
В 1985 г. Скооф представил алгоритм, работающий за полимиальное время, для подсчета 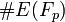 , число точек эллиптической кривой определенная над полем Fp. Алгоритм Скоофа является достаточно не эффективным на практике для значений p, которые действительно представляют интерес, то есть p > 2. В последние несколько лет было проделано много работы по улучшению и ускорению алгоритма Скоофа, сейчас он называется SEA алгоритм. С такими улучшениями криптографически пригодные эллиптические кривые, определенные над полями, чьи порядки более, чем 2, могут быть сгенерированы за несколько часов на рабочих станциях. , число точек эллиптической кривой определенная над полем Fp. Алгоритм Скоофа является достаточно не эффективным на практике для значений p, которые действительно представляют интерес, то есть p > 2. В последние несколько лет было проделано много работы по улучшению и ускорению алгоритма Скоофа, сейчас он называется SEA алгоритм. С такими улучшениями криптографически пригодные эллиптические кривые, определенные над полями, чьи порядки более, чем 2, могут быть сгенерированы за несколько часов на рабочих станциях.
Просмотров: 4726
|
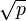
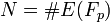 ;
;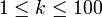 . Если нет, то нужно вернуться на шаг 1;
. Если нет, то нужно вернуться на шаг 1;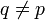 . Если нет, то нужно вернуть на шаг 1;
. Если нет, то нужно вернуть на шаг 1;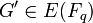 и положить G =G'. Повторяем до тех пор пока
и положить G =G'. Повторяем до тех пор пока 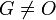 .
.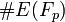 , число точек эллиптической кривой определенная над полем Fp. Алгоритм Скоофа является достаточно не эффективным на практике для значений p, которые действительно представляют интерес, то есть p > 2. В последние несколько лет было проделано много работы по улучшению и ускорению алгоритма Скоофа, сейчас он называется SEA алгоритм. С такими улучшениями криптографически пригодные эллиптические кривые, определенные над полями, чьи порядки более, чем 2, могут быть сгенерированы за несколько часов на рабочих станциях.
, число точек эллиптической кривой определенная над полем Fp. Алгоритм Скоофа является достаточно не эффективным на практике для значений p, которые действительно представляют интерес, то есть p > 2. В последние несколько лет было проделано много работы по улучшению и ускорению алгоритма Скоофа, сейчас он называется SEA алгоритм. С такими улучшениями криптографически пригодные эллиптические кривые, определенные над полями, чьи порядки более, чем 2, могут быть сгенерированы за несколько часов на рабочих станциях.