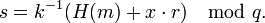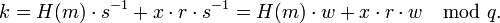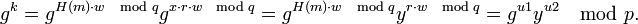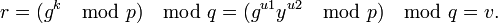Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - DSA - Подпись сообщения29 мая 2011Оглавление: 1. DSA 2. Параметры схемы цифровой подписи 3. Подпись сообщения 4. Реализация алгоритма 5. Генерация псевдопростых чисел для использования в алгоритме 6. Генерация псевдослучайных чисел для использования в алгоритме Подпись сообщения выполняется по следующему алгоритму: 1 Выбор случайного числа Подписью является пара чисел, общая длина подписи 2*N. Проверка подписиПроверка подписи выполняется по алгоритму: 1 Вычисление Подпись верна, если v = r Корректность схемыДанная схема цифровой подписи корректна в той степени, что желающий проверить подлинность подписи всегда получит положительный результат в случае подлинности. Покажем это: Во-первых, если Для подписи сообщения вычисляется Из этого следует Так как g имеет порядок q, получим Наконец, корректность схемы DSA следует из Поскольку фактически подписывается не само сообщение, а его хеш, то очевидно, что несколько различных сообщений могут иметь одинаковую подпись. Это связано с наличием у хеш-функций коллизий. Просмотров: 7416
|
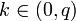 2 Вычисление
2 Вычисление 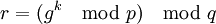 3 Вычисление
3 Вычисление 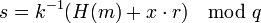 4 Выбор другого k, если оказалось, что r=0 или s=0
4 Выбор другого k, если оказалось, что r=0 или s=0
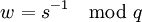 2 Вычисление
2 Вычисление 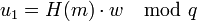 3 Вычисление
3 Вычисление 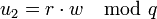 4 Вычисление
4 Вычисление 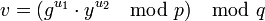
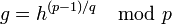 , то из этого по Малой теореме Ферма следует
, то из этого по Малой теореме Ферма следует 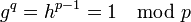 . Поскольку g>1 и q простое число, то g должно иметь мультипликативный порядок q по модулю p.
. Поскольку g>1 и q простое число, то g должно иметь мультипликативный порядок q по модулю p.