Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - DSA - Генерация псевдопростых чисел для использования в алгоритме29 мая 2011Оглавление: 1. DSA 2. Параметры схемы цифровой подписи 3. Подпись сообщения 4. Реализация алгоритма 5. Генерация псевдопростых чисел для использования в алгоритме 6. Генерация псевдослучайных чисел для использования в алгоритме При работе алгоритма DSA требуется два простых числа, следовательно необходим генератор псевдослучайных псевдопростых чисел. В соответствии с DSS псевдопростые числа должны генерироваться с помощью методов, безопасность которых подтверждена в документах FIPS. Один из таких методов описан в дополнении к документу FIPS 186. При этом для проверки на простоту рекомендовано использовать вероятностный тест Миллера — Рабина. Простые числа должны удовлетворять условиям:
Для генерации обоих чисел используется начальное число, которое может определяться уникальными данными домена, для которого планируется генерация доменных параметров, или быть случайным. Рекомендованный алгоритм генерацииПусть L представлена в виде L − 1 = n * N + b, где n и b — целые числа, причем b лежит в диапазоне от 0 включая до N. Генерация псевдопростых чисел p и q выполняется следующим образом: 1. Выбор битовой последовательности длиной от N, далее обозначаемой SEED. Обозначим длину этой последовательности в битах seedlen. 2. Вычисляем Просмотров: 7420
|
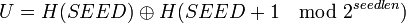 3. Формирование числа q из числа U путем выставления младшего и старшего значащих бит в 1. Что значит побитовое булево сложение с числами 1 и 2. Заметим, что при этом 2 < q < 2.
4. Проверка, является ли полученное q простым.
5. Если окажется, что q составное, то переход на шаг 1
6. Введем переменные counter = 0 и offset = 2.
7. Для всех k = 0,...,n вычислим
3. Формирование числа q из числа U путем выставления младшего и старшего значащих бит в 1. Что значит побитовое булево сложение с числами 1 и 2. Заметим, что при этом 2 < q < 2.
4. Проверка, является ли полученное q простым.
5. Если окажется, что q составное, то переход на шаг 1
6. Введем переменные counter = 0 и offset = 2.
7. Для всех k = 0,...,n вычислим 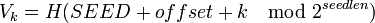 .
8. Введем целое число
.
8. Введем целое число 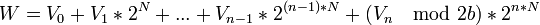 и число X = W + 2. Отметим, что 0 < = W < 2, следовательно 2 < = X < 2L.
9. Пусть
и число X = W + 2. Отметим, что 0 < = W < 2, следовательно 2 < = X < 2L.
9. Пусть 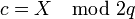 и p = X −. При этом
и p = X −. При этом 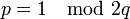 .
10. Если p < 2, то переходим на шаг 13.
11. Проверка p на простоту.
12. Если p проходит тест на простоту, то переходим на шаг 15.
13. Выполнение операций counter = counter + 1 и offset = offset + n + 1.
14. Если counter > = 2 = 4096, то переходим на шаг 1, иначе переход на шаг 7.
15. Запоминаем значения SEED и counter для последующего использования.
.
10. Если p < 2, то переходим на шаг 13.
11. Проверка p на простоту.
12. Если p проходит тест на простоту, то переходим на шаг 15.
13. Выполнение операций counter = counter + 1 и offset = offset + n + 1.
14. Если counter > = 2 = 4096, то переходим на шаг 1, иначе переход на шаг 7.
15. Запоминаем значения SEED и counter для последующего использования.