|
|
|
Компьютеры - Дискретное логарифмирование - Пример23 января 2011
Оглавление:
1. Дискретное логарифмирование
2. Пример
3. Вычислительная сложность и приложения в криптографии
Проще всего рассмотреть задачу дискретного логарифмирования в кольце вычетов по модулю простого числа.
Пусть задано сравнение
Будем решать задачу методом перебора. Выпишем таблицу всех степеней числа 3. Каждый раз мы вычисляем остаток от деления на 17.
| 3 ≡ 3 |
3 ≡ 9 |
3 ≡ 10 |
3 ≡ 13 |
3 ≡ 5 |
3 ≡ 15 |
3 ≡ 11 |
3 ≡ 16 |
| 3 ≡ 14 |
3 ≡ 8 |
3 ≡ 7 |
3 ≡ 4 |
3 ≡ 12 |
3 ≡ 2 |
3 ≡ 6 |
3 ≡ 1 |
Теперь легко увидеть, что решением рассматриваемого сравнения является x=4, поскольку 3≡13.
На практике модуль обычно является достаточно большим числом, и метод перебора является слишком медленным, поэтому возникает потребность в более быстрых алгоритмах.
Алгоритмы решения
В произвольной мультипликативной группе
Разрешимости и решению задачи дискретного логарифмирования в произвольной конечной абелевой группе посвящена статья J. Buchmann, M. J. Jacobson и E. Teske. В алгоритме используется таблица, состоящая из 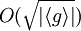 пар элементов и выполняется пар элементов и выполняется 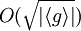 умножений. Данный алгоритм медленный и не пригоден для практического использования. Для конкретных групп существуют свои, более эффективные, алгоритмы. умножений. Данный алгоритм медленный и не пригоден для практического использования. Для конкретных групп существуют свои, более эффективные, алгоритмы.
В кольце вычетов по простому модулю
Рассмотрим уравнение
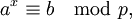 |
) |
где p - простое, b не делится на p. Если a является образующим элементом группы 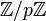 , то уравнение имеет решение при любых b. Такие числа a называются ещё первообразными корнями, и их количество равно φ, где φ — функция Эйлера. Решение уравнения можно находить по формуле: , то уравнение имеет решение при любых b. Такие числа a называются ещё первообразными корнями, и их количество равно φ, где φ — функция Эйлера. Решение уравнения можно находить по формуле:
Однако, сложность вычисления по этой формуле хуже, чем сложность перебора.
Следующий алгоритм имеет сложность 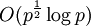
Алгоритм
- Присвоить
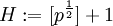
- Найти

- Составить таблицу значений
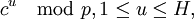 и упорядочить её. и упорядочить её.
- Составить таблицу значений
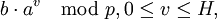 и упорядочить её. и упорядочить её.
- Найти совпавшие элементы из первой и второй таблиц. Для них
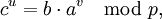
откуда 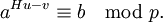
- Выдать
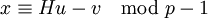 . .
Конец алгоритма
Существует также множество других алгоритмов для решения задачи дискретного логарифмирования в поле вычетов. Их принято разделять на экспоненциальные и субэкспоненциальные. Полиномиального алгоритма для решения этой задачи пока не существует.
Алгоритмы с экспоненциальной сложностью
- Алгоритм Шенкса
- Алгоритм Полига-Хеллмана — работает, если известно разложение числа
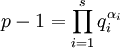 на простые множители. Сложность: на простые множители. Сложность: 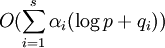 . Если множители, на которые раскладывается p − 1, достаточно маленькие, то алгоритм очень эффективен. . Если множители, на которые раскладывается p − 1, достаточно маленькие, то алгоритм очень эффективен.
- ρ-метод Полларда имеет эвристическую оценку сложности
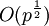 . .
Субэкспоненциальные алгоритмы
Данные алгоритмы имеют сложность 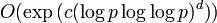 арифметических операций, где арифметических операций, где  и и 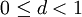 — некоторые константы. Эффективность алгоритма во многом зависит от близости c к 1 и d — к 0. — некоторые константы. Эффективность алгоритма во многом зависит от близости c к 1 и d — к 0.
- Алгоритм Адлемана появился в 1979 году. Это был первый субэкспоненциалный алгоритм дискретного логарифмирования. На практике он всё же недостаточно эффективен. В этом алгоритме
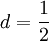 . .
- Алгоритм COS был предложен в 1986 году математиками Копперсмитом, Одлыжко и Шреппелем. В этом алгоритме константа
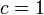 , , 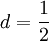 . В 1991 году с помощью этого метода было проведено логарифмирование по модулю . В 1991 году с помощью этого метода было проведено логарифмирование по модулю 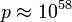 . В 1997 году Вебер провел дискретное логарифмирование по модулю . В 1997 году Вебер провел дискретное логарифмирование по модулю 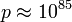 с помощью некоторой версии данного алгоритма. Экспериментально показано, что при с помощью некоторой версии данного алгоритма. Экспериментально показано, что при 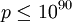 алгоритм COS лучше решета числового поля. алгоритм COS лучше решета числового поля.
- Решето числового поля было применено к дискретному логарифмированию позднее, чем к факторизации чисел. Первые идеи появились в 1990-х годах. Алгоритм, предложенный Д. Гордоном в 1993 году, имел эвристическую сложность
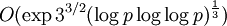 , но оказался достаточно непрактичным. Позднее было предложено множество различных улучшений данного алгоритма. Было показано, что при , но оказался достаточно непрактичным. Позднее было предложено множество различных улучшений данного алгоритма. Было показано, что при 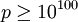 решето числового поля быстрее, чем COS. Современные рекорды в дискретном логарифмировании получены именно с помощью этого метода. решето числового поля быстрее, чем COS. Современные рекорды в дискретном логарифмировании получены именно с помощью этого метода.
Наилучшими параметрами в оценке сложности на данный момент является 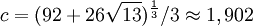 , , 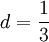 . .
Для чисел специального вида результат можно улучшить. В некоторых случаях можно построить алгоритм, для которого константы будут 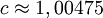 , , 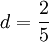 . За счёт того, что константа c достаточно близка к 1, подобные алгоритмы могут обогнать алгоритм с . За счёт того, что константа c достаточно близка к 1, подобные алгоритмы могут обогнать алгоритм с 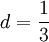 . .
В произвольном конечном поле
Задача рассматривается в поле GF, где q = p, p — простое.
- Алгоритм исчисления индексов эффективен, если p невелико. В этом случае он имеет эвристическую оценку сложности
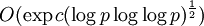 . .
- Алгоритм Эль-Гамаля, появившийся в 1985 году, применим при n = 2 и имеет сложность
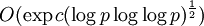 арифметических операций. арифметических операций.
- Алгоритм Копперсмита дискретного логарифмирования в конечном поле характеристики 2 стал первым субэкспоненциальным алгоритмом дискретного логарифмирования с константой
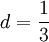 в оценки сложности. Данный алгоритм появился в 1984 году — до изобретения решета числового поля. в оценки сложности. Данный алгоритм появился в 1984 году — до изобретения решета числового поля.
В группе точек на эллиптической кривой
Рассматривается группа точек эллиптической кривой над конечным полем. В данной группе определена операция сложения двух точек. Тогда mP — это 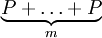 . Решением задачи дискретного логарифмирования на эллиптической кривой является нахождение такого натурального числа m, что . Решением задачи дискретного логарифмирования на эллиптической кривой является нахождение такого натурального числа m, что
для заданных точек P и A.
До 1990 года не существовало алгоритмов дискретного логарифмирования, учитывающих особенностей строения группы точек эллиптической кривой. Впоследствии, Менезес, Окамото и Венстон предложили алгоритм, использующий спаривание Вейля. Для эллиптической кривой, определённой над полем GF, данный алгоритм сводит задачу дискретного логарифмирования к аналогичной задаче в поле GF. Однако, данное сведение полезно, только если степень k мала. Это условие выполняется, в основном, для суперсингулярных эллиптических кривых. В остальных случаях подобное сведение практически никогда не приводит к субэкспоненциальным алгоритмам.
Просмотров: 5419
|
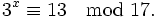
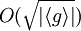 пар элементов и выполняется
пар элементов и выполняется 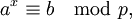
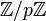 , то уравнение имеет решение при любых b. Такие числа a называются ещё первообразными корнями, и их количество равно φ, где φ — функция Эйлера. Решение уравнения можно находить по формуле:
, то уравнение имеет решение при любых b. Такие числа a называются ещё первообразными корнями, и их количество равно φ, где φ — функция Эйлера. Решение уравнения можно находить по формуле: 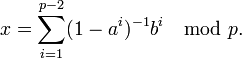
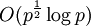
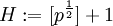

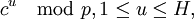 и упорядочить её.
и упорядочить её.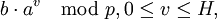 и упорядочить её.
и упорядочить её.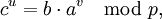
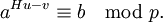
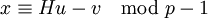 .
.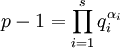 на простые множители. Сложность:
на простые множители. Сложность: 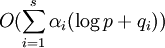 . Если множители, на которые раскладывается p − 1, достаточно маленькие, то алгоритм очень эффективен.
. Если множители, на которые раскладывается p − 1, достаточно маленькие, то алгоритм очень эффективен.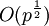 .
.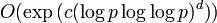 арифметических операций, где
арифметических операций, где  и
и 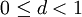 — некоторые константы. Эффективность алгоритма во многом зависит от близости c к 1 и d — к 0.
— некоторые константы. Эффективность алгоритма во многом зависит от близости c к 1 и d — к 0.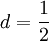 .
.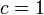 ,
, 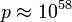 . В 1997 году Вебер провел дискретное логарифмирование по модулю
. В 1997 году Вебер провел дискретное логарифмирование по модулю 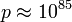 с помощью некоторой версии данного алгоритма. Экспериментально показано, что при
с помощью некоторой версии данного алгоритма. Экспериментально показано, что при 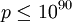 алгоритм COS лучше решета числового поля.
алгоритм COS лучше решета числового поля.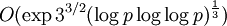 , но оказался достаточно непрактичным. Позднее было предложено множество различных улучшений данного алгоритма. Было показано, что при
, но оказался достаточно непрактичным. Позднее было предложено множество различных улучшений данного алгоритма. Было показано, что при 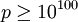 решето числового поля быстрее, чем COS. Современные рекорды в дискретном логарифмировании получены именно с помощью этого метода.
решето числового поля быстрее, чем COS. Современные рекорды в дискретном логарифмировании получены именно с помощью этого метода.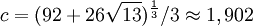 ,
, 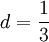 .
.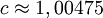 ,
, 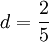 . За счёт того, что константа c достаточно близка к 1, подобные алгоритмы могут обогнать алгоритм с
. За счёт того, что константа c достаточно близка к 1, подобные алгоритмы могут обогнать алгоритм с 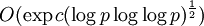 .
.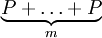 . Решением задачи дискретного логарифмирования на эллиптической кривой является нахождение такого натурального числа m, что
. Решением задачи дискретного логарифмирования на эллиптической кривой является нахождение такого натурального числа m, что