Интернет магазин китайских планшетных компьютеров

Компьютеры - Дискретное логарифмирование

Дискретное логарифмирование – задача обращения функции g в некоторой конечной мультипликативной группе G.

Наиболее часто задачу дискретного логарифмирования рассматривают в мультипликативной группе кольца вычетов или конечного поля, а также в группе точек эллиптической кривой над конечным полем. Эффективные алгоритмы для решения задачи дискретного логарифмирования в общем случае неизвестны.

Для заданных g и a решение x уравнения g = a называется дискретным логарифмом элемента a по основанию g. В случае, когда G является мультипликативной группой кольца вычетов по модулю m, решение называют также индексом числа a по основанию g. Индекс числа a по основанию g гарантированно существует, если g является первообразным корнем по модулю m.

Постановка задачи

Пусть в некоторой конечной мультипликативной абелевой группе G задано уравнение

Решение задачи дискретного логарифмирования состоит в нахождении некоторого целого неотрицательного числа x, удовлетворяющего уравнению. Если оно разрешимо, у него должно быть хотя бы одно натуральное решение, не превышающее порядок группы. Это сразу даёт грубую оценку сложности алгоритма поиска решений сверху — алгоритм полного перебора нашел бы решение за число шагов не выше порядка данной группы.

Чаще всего рассматривается случай, когда 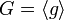, то есть группа является циклической, порождённой элементом g. В этом случае уравнение всегда имеет решение. В случае же произвольной группы вопрос о разрешимости задачи дискретного логарифмирования, то есть вопрос о существовании решений уравнения, требует отдельного рассмотрения.