Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Диаграмма Вороного - Обобщения23 января 2011Оглавление: 1. Диаграмма Вороного 2. Алгоритмы построения 3. Обобщения 4. Применение Диаграмму Вороного очевидным образом можно определить для множества точек в произвольном евклидовом пространстве, необязательно двумерном. Имеет место следующее утверждение: в k-мерном пространстве количество симплексов k-мерной триангуляции Делоне множества из n точек может достигать Диаграмма Вороного может быть определена для пространства с метрикой, отличной от евклидовой. Однако в этом случае границы между соседними областями Вороного могут не быть многообразиями первого порядка. Множество S может состоять не только из точек, но и из любых объектов, для которых определено расстояние до произвольной точки плоскости. В этом случае элементы множества S называют сайтами. В качестве примера можно привести диаграмму Вороного многоугольника, где в роли сайтов выступают вершины и рёбра многоугольника. Такие диаграммы используются для построения срединных осей и широко применяются в задачах анализа изображений. Граница областей диаграммы Вороного многоугольника представляет собой объединение отрезков прямых и парабол. Просмотров: 6852
|
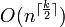 . Следовательно, такой же порядок имеют расходы памяти, требуемой для хранения двойственной диаграммы Вороного.
. Следовательно, такой же порядок имеют расходы памяти, требуемой для хранения двойственной диаграммы Вороного.