Интернет магазин китайских планшетных компьютеров

Компьютеры - Диаграмма Вороного - Алгоритмы построения

Построение диаграммы алгоритмом Форчуна.

Простой алгоритм

Рассмотрим серединный перпендикуляр отрезка, соединяющего некоторую пару точек p и q. Этот перпендикуляр разбивает плоскость на две полуплоскости H_pq и H_qp, причём область Вороного точки p целиком содержится в одной из них, а область точки q — в другой. Область Вороного V_p точки p совпадает с пересечением всех таких полуплоскостей H_pq:

.

Таким образом, решение задачи сводится к вычислению такого пересечения для каждой точки p. Алгоритм может быть реализован с вычислительной сложностью O.

Алгоритм Форчуна

Алгоритм основан на применении заметающей прямой. Заметающая прямая — это вспомогательный объект, представляющий собой вертикальную прямую линию. На каждом шаге алгоритма диаграмма Вороного построена для множества, состоящего из заметающей прямой и точек слева от неё. При этом граница между областью Вороного прямой и областями точек состоит из отрезков парабол. Прямая движется слева направо. Каждый раз, когда она проходит через очередную точку, эта точка добавляется к уже построенному участку диаграммы. Добавление точки к диаграмме при использовании двоичного дерева поиска имеет сложность O, всего точек n, а сортировка точек по x-координате может быть выполнена за O, поэтому вычислительная сложность алгоритма Форчуна равна O.

Рекурсивный алгоритм

Основная идея рекурсивного алгоритма заключается в использовании метода динамического программирования. Исходное множество точек S разбивается на два подмножества S₁ и S₂, для каждого из них строится диаграмма Вороного, а затем полученные диаграммы объединяются в одну. Разбиение множества S осуществляется при помощи прямой, разделяющей плоскость на две полуплоскости, так, чтобы в обеих полуплоскостях находилось примерно одинаковое количество точек. Объединение диаграмм Вороного множеств S₁ и S₂ может быть выполнено за время O, поэтому вычислительная сложность алгоритма равна O.
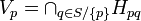