01 мая 2011
Оглавление:
1. Coq
2. Примеры
3. Инструменты
4. Язык
5. Библиотеки и приложения
Ассоциативность композиции функций
Доказательство «на бумаге».
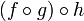
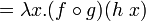 ; δ-эквивалентность ; δ-эквивалентность
 ; δ-эквивалентность ; δ-эквивалентность
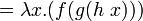 ; β-эквивалентность ; β-эквивалентность
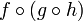
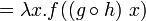 ; δ-эквивалентность ; δ-эквивалентность
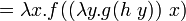 ; δ-эквивалентность ; δ-эквивалентность
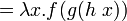 ; β-эквивалентность ; β-эквивалентность
По транзитивности равенства
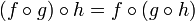
Доказательство в Coq.
Definition cf := fun t0 t1 t2 : Type
=> fun => fun x => f.
Implicit Arguments cf.
Notation "f @ g" :=.
Definition cf_assoc := fun
=> : @ h = f @.
cf — определение композиции функций. Notation вводит инфиксное обозначение @ для композиции функций.
cf_assoc — собственно доказательство. Coq основан на изоморфизме Карри-Говарда, поэтому доказательство есть терм лямбда-исчисления.
fun … => … в Coq обозначает лямбда-абстракцию. Функциям даются имена f, g, h, а их областям определения и областям значений даются имена t0, t1, t2, t3.
Кроме лямбда-абстракции доказательство состоит из refl_equal — аксиомы рефлексивности равенства. Нам нужно привести левую и правую части равенства с помощью βδ-редукций к одному выражению. Coq сам выполняет βδ-редукцию, поэтому доказательство практически пустое.
Чтобы понять роль refl_equal, выполните Check. Coq покажет автоматически выведенный тип этого терма, а именно, 2 = 2. Но в доказательстве cf_assoc аргумент refl_equal заменён на подчёркивание. Coq сам может вывести этот аргумент. Это сокращает объём доказательства. Выполнив Print cf_assoc., можно убедиться, что Coq вывел терм @ h вместо подчёркивания.
Коммутативность умножения в арифметике Пеано
Тип натуральных чисел определён в стандартной библиотеке так:
Inductive nat : Set :=
| O : nat
| S : nat -> nat.
O есть ноль и S есть функция, возвращающая следующее число.
Необходимо доказать, что  . Доказательство строится с помощью математической индукции по одному из множителей. . Доказательство строится с помощью математической индукции по одному из множителей.
Доказательство «на бумаге»
Будут использоваться обозначения, принятые в Coq, чтобы было легче сопоставить оба доказательства.
Выполним индукцию по n.
База индукции: доказать 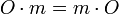 . Высказывание . Высказывание 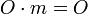 следует из βδι-преобразования. следует из βδι-преобразования. 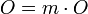 доказывается отдельной леммой. доказывается отдельной леммой.
Шаг индукции: имея индуктивную гипотезу  , доказать , доказать 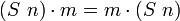 . Из βδι-преобразования следует . Из βδι-преобразования следует 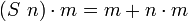 . Имеется лемма, которая утверждает . Имеется лемма, которая утверждает 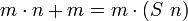 . Используем коммутативность сложения и индуктивную гипотезу. . Используем коммутативность сложения и индуктивную гипотезу.
Доказательство в Coq
Следующее доказательство скопировано с небольшими изменениями из стандартной библиотеки. Оно использует тактики.
Тактика автоматически генерирует доказательство, опираясь на цель. Конечно, должен существовать алгоритм поиска доказательства. В некоторых случаях тактики могут сильно уменьшить объём доказательства.
Чтобы использовать тактики, необходимо после Definition указать тип, но опустить лямбда-терм, то есть само доказательство. Тогда Coq переходит в «proof editing mode», где можно построить доказательство с помощью тактик.
Если тактика смогла полностью доказать цель, она генерирует ноль подцелей. Если тактика не смогла довести доказательство до конца, хотя и выполнила некоторые шаги, то тактика генерирует ненулевое количество подцелей. Чтобы завершить доказательство, нужно доказать подцели с помощью других тактик. Таким образом можно комбинировать разные тактики.
«Proof editing mode» не запрещает строить доказательство как лямбда-терм. Тактика refine доказать цель с помощью указанного после refine лябмда-терма. refine имеет следующую дополнительную возможность: если в лябмда-терме вместо некоторых подтермов стоит подчёркивание и Coq не может вывести значение подтермов автоматически, то это подчёркивание генерирует подцель. Таким образом, refine может генерировать произвольное количество подцелей.
Require Import Coq.Arith.Plus.
Definition mult_comm : forall n m, n * m = m * n.
Proof.
intros. elim n.
auto with arith.
intros. simpl in |- *. elim mult_n_Sm. elim H. apply plus_comm.
Qed.
intros вводит предпосылки. elim применяет математическую индукцию, после чего цель доказательства разбивается на две подцели: база и шаг индукции. auto with arith доказывает базу индукции; тактика auto ищет простым перебором подходящую теорему в базе данных теорем и подставляет её в доказательство. В данном случае она находит лемму mult_n_O. В этом можно убедиться, выполнив Show Proof. При доказательстве шага индукции применяются леммы mult_n_Sm, plus_comm, и индуктивная гипотеза H. Имя индуктивной гипотезы было сгенерировано автоматически тактикой intros, второе вхождение тактики. simpl in |- * выполняет βδι-преобразование цели. Хотя она не генерирует доказательства, но она приводит цель к такому виду, который нужен для вывода аргументов тактикой apply plus_comm.
То же доказательство можно выразить лямбда-термом.
Definition mult_comm := fun n:nat
=> fix rec
: n * m = m * n
:= match m as m return n * m = m * n with
| O => sym_eq
| S pm => match rec pm in _ = dep return _ = n + dep
with refl_equal =>
match mult_n_Sm _ _ in _ = dep return dep = _
with refl_equal => plus_comm _ _ end
end
end.
elim n соответствует fix … match … as …. Остальные elim соответствуют match … in _=dep …. В доказательстве с помощью тактик нет нужды указывать конструкторы O и S, так как они выводятся из nat.
Definition mult_comm := fun n:nat
=> nat_ind
)
(fun _ rec =>
eq_ind _
_)
_ rec).
Это более компактная, хотя менее наглядная запись. nat_ind и eq_ind называются принципами индукции и являются функциями, сгенерированными согласно структуре индуктивных типов. Тактики вставляют в доказательство именно эти функции.
Как видно, тактики позволяют опускать множество термов, которые можно вывести автоматически.
Коммутативность умножения в кольце Гротендика
Это пример использования специализированной тактики ring. Она выполняет преобразования формул, построенных из операций полукольца или кольца.
Кольцо Гротендика конструируется из полукольца следующим образом. int_bipart — носитель кольца — есть вторая декартова степень nat — носителя полукольца.
Record int_bipart : Set := {pneg : nat; ppos : nat}.
Record не только конструирует декартово произведение множеств, но и генерирует левую и правую проекции. Значение i из множества int_bipart можно понимать как решение уравнения 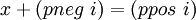 , где x — неизвестная величина. Если , где x — неизвестная величина. Если 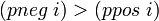 , то решение является отрицательным числом. , то решение является отрицательным числом.
Сложение в кольце определено как покомпонентное сложение, то есть pneg левого слагаемого складывается с pneg правого слагаемого, ppos левого слагаемого складывается с ppos правого слагаемого.
Notation "a !+ b" :=.
Definition plus a b := Build_int_bipart
.
Notation "a + b" :=.
Мы обозначаем сложение в полукольце как «!+» и сложение в кольце как «+».
Умножение определяется так: в часть pneg идут произведения разных компонент, в часть ppos идут произведения одинаковых компонент.
Notation "a !* b" :=.
Definition mult a b := Build_int_bipart
.
Notation "a * b" :=.
Мы обозначаем умножение в полукольце как «!*» и умножение в кольце как «*».
Сначала докажем лемму «если оба компонента int_bipart равны, то int_bipart равны».
Definition int_bipart_eq_part
: forall an bn, an = bn -> forall ap bp, ap = bp
-> Build_int_bipart an ap = Build_int_bipart bn bp.
Proof.
refine.
refine _ _ eqn).
refine.
Qed.
Теперь докажем коммутативность умножения в кольце, то есть n * m = m * n.
Require Import ArithRing.
Definition mult_comm : forall n m, n * m = m * n.
Proof.
refine; simpl; ring.
Qed.
Нужно доказать равенство двух int_bipart. Лемма int_bipart_eq_part разбивает нашу цель на две подцели. Первая подцель есть равенство компонент pneg, вторая подцель есть равенство компонент ppos. Увидеть эти подцели можно, если сразу после Proof. выполнить refine. «;» между refine и означает, что комбинированная тактика доказывает все подцели, генерируемые тактикой refine.
Чтобы доказать «на бумаге», нужно последовательно применить свойства операций полукольца:
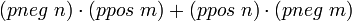
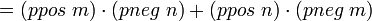 ; коммутативность умножения ; коммутативность умножения
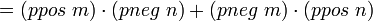 ; коммутативность умножения ; коммутативность умножения
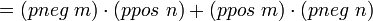 ; коммутативность сложения ; коммутативность сложения
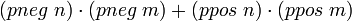
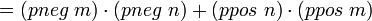 ; коммутативность умножения ; коммутативность умножения
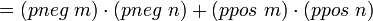 ; коммутативность умножения ; коммутативность умножения
Тактика ring генерирует все эти преобразования автоматически.
Просмотров: 4435
|
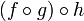
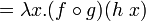 ; δ-эквивалентность
; δ-эквивалентность ; δ-эквивалентность
; δ-эквивалентность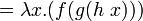 ; β-эквивалентность
; β-эквивалентность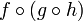
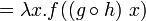 ; δ-эквивалентность
; δ-эквивалентность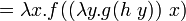 ; δ-эквивалентность
; δ-эквивалентность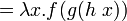 ; β-эквивалентность
; β-эквивалентность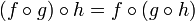
 . Доказательство строится с помощью математической индукции по одному из множителей.
. Доказательство строится с помощью математической индукции по одному из множителей.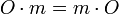 . Высказывание
. Высказывание 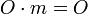 следует из βδι-преобразования.
следует из βδι-преобразования. 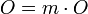 доказывается отдельной леммой.
доказывается отдельной леммой.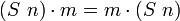 . Из βδι-преобразования следует
. Из βδι-преобразования следует 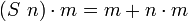 . Имеется лемма, которая утверждает
. Имеется лемма, которая утверждает 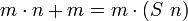 . Используем коммутативность сложения и индуктивную гипотезу.
. Используем коммутативность сложения и индуктивную гипотезу.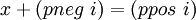 , где x — неизвестная величина. Если
, где x — неизвестная величина. Если 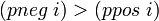 , то решение является отрицательным числом.
, то решение является отрицательным числом.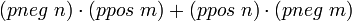
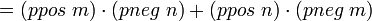 ; коммутативность умножения
; коммутативность умножения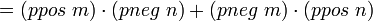 ; коммутативность умножения
; коммутативность умножения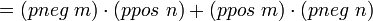 ; коммутативность сложения
; коммутативность сложения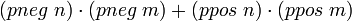
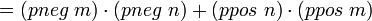 ; коммутативность умножения
; коммутативность умножения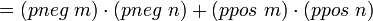 ; коммутативность умножения
; коммутативность умножения