|
|
|
Компьютеры - CBC-MAC - Предложенная спецификация16 июня 2011
Оглавление:
1. CBC-MAC
2. Обозначения
3. Основная конструкция семейства ОМАС
4. Предложенная спецификация
5. Безопасность семейства OMAC
6. Аналоги
В OMAC1 положим Cst = 0, HL = L•x, Cst1 = u и Cst2 = u, где «•» означает умножение в GF. L = EK, 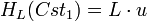 и и 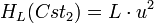 равносильны. OMAC2 аналогичен OMAC1, исключая Cst2 = u вместо Cst2 = u. L = EK, равносильны. OMAC2 аналогичен OMAC1, исключая Cst2 = u вместо Cst2 = u. L = EK, 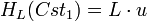 и и  равносильны. Кроме того, равносильны. Кроме того, 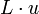 , , 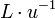 и и 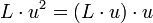 могут быть эффективно вычислены с помощью одного сдвига и одной операции XOR от L и могут быть эффективно вычислены с помощью одного сдвига и одной операции XOR от L и 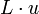 , соответственно как показано в и. Легко заметить, что условия в Sec. 3 выполняются для ε1 = ... = ε6 = 2 − n в OMAC1 и OMAC2. OMAC1 и OMAC2 проиллюстрированы на Рис.2 и описываются следующим образом: , соответственно как показано в и. Легко заметить, что условия в Sec. 3 выполняются для ε1 = ... = ε6 = 2 − n в OMAC1 и OMAC2. OMAC1 и OMAC2 проиллюстрированы на Рис.2 и описываются следующим образом:
1. Для OMAC1:
Algorithm OMAC1K
L ← EK;
Y ← 0;
Partition M into M ... M
for i ← 1 to m − 1 do
X ← M ⊕ Y;
if |M| = n
then X ← X ⊕ 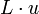 ; ;
else Y ← E_k;
X ← padn ⊕ Y;
if |M| = n then X ← X ⊕ 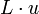 ; ;
else X ← X ⊕ 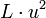 ; ;
T ← EK;
return T;
1. Для OMAC2:
Algorithm OMAC2K
L ← EK;
Y ← 0;
Partition M into M ... M
for i ← 1 to m − 1 do
X ← M ⊕ Y;
if |M| = n
then X ← X ⊕ 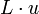 ; ;
else Y ← E_k;
X ← padn ⊕ Y;
if |M| = n then X ← X ⊕ 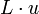 ; ;
else X ← X ⊕ 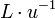 ; ;
T ← EK;
return T;
Просмотров: 5836
|
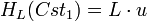 и
и 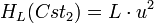 равносильны. OMAC2 аналогичен OMAC1, исключая Cst2 = u вместо Cst2 = u. L = EK,
равносильны. OMAC2 аналогичен OMAC1, исключая Cst2 = u вместо Cst2 = u. L = EK,  равносильны. Кроме того,
равносильны. Кроме того, 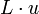 ,
, 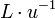 и
и 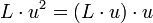 могут быть эффективно вычислены с помощью одного сдвига и одной операции XOR от L и
могут быть эффективно вычислены с помощью одного сдвига и одной операции XOR от L и 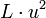 ;
;