Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - CBC-MAC - Обозначения16 июня 2011Оглавление: 1. CBC-MAC 2. Обозначения 3. Основная конструкция семейства ОМАС 4. Предложенная спецификация 5. Безопасность семейства OMAC 6. Аналоги Для набора A, x←A означает, что x выбирается из A случайно, причём выбор любого значения из набора А является равновероятным. Если a, b равновеликие строки, тогда a ⊕ b является их побитовой операцией XOR. Если a, b не равновеликие строки, то a ◦ b обозначает их конкатенацию.. Для n-битной строки a = an − 1...a1a0 ∈ {0, 1}*, обозначим a << 1 = an − 2...a1a00 n-битную строку, которая сдвинута влево на 1 бит, в это же время обозначим a >> 1 = 0an − 1...a2a1 n-битную строку, которая сдвинута вправо на один бит. Если a ∈ {0, 1}* является строкой, то |a| обозначим её битовую длину. Для любого бита строка a ∈ {0, 1}* такова что |a| ≤ n, положим что CBC MACБлочный шифр Е является функцией Е : KE × {0,1} → {0,1}, где каждое E = EK является перестановкой {0,1}, в свою очередь KE является набором всевозможных ключей, а n — длина блока. CBC MAC является наипростейшим и наиболее известным алгоритмом, для того что бы сделать MAC из блочного шифра Е. Пусть сообщение будет иметь вид M = M ◦M ◦ … ◦M, где |M| = |M| = … = |M| = n. Тогда CBCK, CBC MAC сообщения M при условии ключа K, определяется как Y, где Y = EK для i = 1, … ,m и Y = 0. Bellare, Kilian и Rogaway доказали безопасность CBC MAC для фиксированной длины сообщения в mn бит. Поле с 2 точкамиМы вправе рассматривать точку a в GF любым из следующих способов: как абстрактная точка в поле а; как n-битную строку an − 1...a1a0 ∈ {0,1}; как формальный полином a = an − 1u + ... + a1u + a0 с бинарными коэффициентами. Для того что бы добавить 2 точки в GF, рассмотрим битовую операцию ХOR над ними. Обозначим эту операцию с помощью a ⊕ b. Для того что бы перемножить две точки, зафиксируем некоторый полином f с бинарными коэффициентами и степенью n. Для большей точности, выберем лексикографически первым полином среди таких же полиномов степени n имеющий минимальное число коэффициентов. Перечислим некоторые из указанных полиномов Просмотров: 5837
|
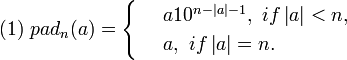
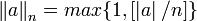 , где пустая строка считается как один блок.
, где пустая строка считается как один блок.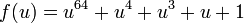 для n = 64,
для n = 64,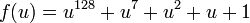 для n = 128, и
для n = 128, и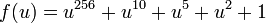 для n = 256.
для n = 256.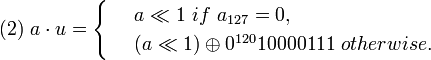
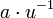 . Например,
. Например,