Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - CBC-MAC - Безопасность семейства OMAC16 июня 2011Оглавление: 1. CBC-MAC 2. Обозначения 3. Основная конструкция семейства ОМАС 4. Предложенная спецификация 5. Безопасность семейства OMAC 6. Аналоги Определение защищённостиПусть Perm означает набор всех перестановок из {0,1}, так же пусть P является случайной перестановкой, если Р — случайная выборка из Perm. Безопасность блочного шифра E может быть количественно определена как
где максимум берётся по всем противникам, кто «работает» не мобее времени t, производит не более q запросов, и кадлый запрос не более μ бит. Будем говорить, MAC алгоритм защищён, если величина пренебрежимо мала. Обозначим Rand набор всех функций из {0, 1}* в {0,1}. Этот набор даётся вероятностной мерой в предположении, что случайный элемент R набора Rand связан или ассоциирован с каждой строкой M ∈ {0, 1}* случайной строки R∈{0,1}. Далее, мы определим преймущество как Далее приведём основные теоремы. Lemma 5.1. Предположим, что H, Cst1 и Cst2 удовлетворяют условиям Sec. 3 для некоторых пренебрежимо малых ε1,...,ε6, а так же пусть Cst — произвольная n-битная константа. Так же предположим, что случайная перестановка P ∈ Perm используется в семействе OMAC как базовый блочный шифр. Пусть A — противник, который делает не более q запросов, и каждый запрос не более nm бит. Положим m ≤ 2n/4. Тогда Lemma 5.2. Предположим, что случайная перестановка P ∈ Perm используется в OMAC как базовый блочный шифр . Пусть A будет противником, который делает не более q запросов, и каждый запрос не более nm бит. Положим m ≤ 2n/4. Тогда Замечание 5.1. Пусть E : KE × {0,1} → {0,1} является базовым блочным шифром, который используется в OMAC. Тогда Просмотров: 5867
|
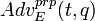 , максимальное преимущество, которое противник A может получить, когда пытается выделить
, максимальное преимущество, которое противник A может получить, когда пытается выделить 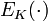 из случайной перестановки P, когда допускается вычисление времени t и q запросов" src="/c/img/10104.png" /> либо
из случайной перестановки P, когда допускается вычисление времени t и q запросов" src="/c/img/10104.png" /> либо 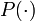 ). Это преимущество определяется следующим образом.
). Это преимущество определяется следующим образом.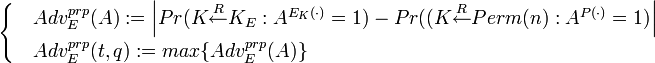
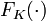 для F. Скажем, что противник
для F. Скажем, что противник 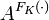 взламывает, если A выдаёт ), где A никогда не запрашивает M из
взламывает, если A выдаёт ), где A никогда не запрашивает M из 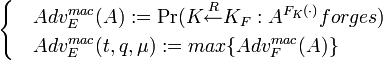
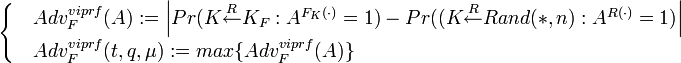
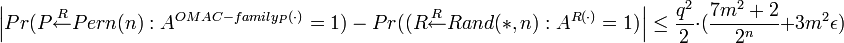
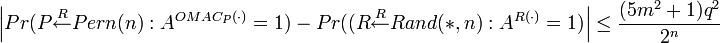
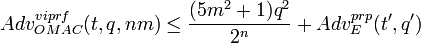 , где t’ = t + O and q’ = mq + 1.
, где t’ = t + O and q’ = mq + 1.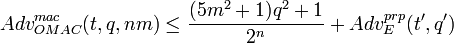 ,
,