Интернет магазин китайских планшетных компьютеров

Компьютеры - CBC-MAC

В криптографии, CBC MAC является технологией построения аутенфикационного кода сообщения из блочного шифра. Сообщение шифруется при помощи некоторого блочного алгоритма шифрования в режиме CBC, для создания цепочки блоков с правилом — каждый блок зависит от надлежащего шифрования предыдущего. Эта взаимозависимость гарантирует, что изменение в любом бите открытого текста приведёт к изменению конечного зашифрованного блока в сторону, которая не может быть предсказана или высчитана в случае, если ключ блочного шифра не известен. Использовался как государственный стандарт США - DAA.

Справочная информация

Алгоритм CBC MAC является хорошо известным методом для генерации имитовставки, основанный на блочном шифре. Bellare, Kilian и Rogaway доказали безопасность алгоритма при фиксированной длине сообщения в m*n бит, где n — длина базового блочного шифра Е. Однако, хорошо известно, что CBC MAC не является безопасным, если длина сообщения не является фиксированной. Таким образом, было предложено несколько вариантов алгоритма для варьируемой длины сообщения. Сначала была предложена зашифрованная имитовставка. Она получается шифрованием CBC MAC значения с помощью E и новым ключом K. 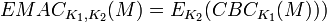То есть , где M — сообщение, K₁ — ключ CBC MAC и 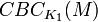— значение CBC MAC сообщения М. Petrank и Rackoff позже доказали, что EMAC защищён, если длина сообщения кратна n. Однако, EMAC требует два ключевых расписания базового блочного шифра E. Далее Black и Rogaway предложили XCBC, который требует только одного ключевого расписания базового блочного шифра E. XCBC даёт три ключа: один ключ блочного шифра K1, и два ключа по n бит. XCBC описывается следующей схемой

На таблице приведено сравнение длин ключей.

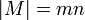Если для некоторого m > 0, то XCBC вычисляется в точности, как и CBC MAC, за исключением операции XOR ключа K₂ до шифрования последнего блока.

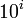В противном случае, добавляется к М и XCBC вычисляется в точности, как и CBC MAC для полученного сообщения. За исключением операции XOR другого ключа K₃ до шифрования последнего блока. Однако, недостатком XCBC заключается в требовании трёх ключей, то есть в сумме бит. В итоге, Kurosawa и Iwata предложили двуключевой CBC MAC. TMAC принимает два ключа, в сумме бит: ключ K₁ блочного шифра и ключ K₂. TMAC получается из XCBC перемещением 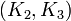на 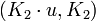, где u — некоторая ненулевая константа, а «•» обозначает умножение в 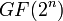. Как уже было сказано, OMAC принимает только один ключ К блочного шифра Е. Длина ключа, k бит, минимальна, так как базовый шифр должен содержать ключ K, состоящий из k бит в любом случае.

OMAC

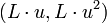OMAC является родительским названием для OMAC1 и OMAC2. OMAC1 получается из XCBC с помощью замены на для некоторой не равной нулю константе u в 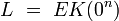, где L — даётся с помощью следующего выражения: . OMAC2 аналогично получается используя 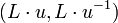. Мы можем вычислть 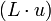, 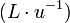и 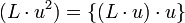эффективно одним сдвигом и условием XOR на 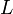и , соответственно. OMAC1 описывается следующей схемой:

1. Если для некоторого m > 0, тогда OMAC вычисляется в точности, как CBC MAC, за исключением операции XOR для до шифрования последнего блока.
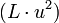2. В противном случае, добавляется к M и OMAC Вычисляется в точности, как CBC MAC для полученного сообщения М, за исключением операции XOR для " src="/c/img/10077.png" /> до шифрования последнего блока.

Кроме того, в TMAC, ключ K₂ является частью ключа, в то время как в OMAC, L не является частью ключа и генерируется из K. Эта сохранность длины ключа делает доказательство безопасности OMAC значительно сложнее чем для TMAC, как показано ниже. На рисунке 2, пусть M = 0. Тогда L является выходом первого E_K. L всегда появляется снова в последнем блоке. В основном, подобное повторное использование L могло бы привести к тупику в доказательстве безопасности. так же используется как ключ универсальной хэш-функции. Однако L появляется как выход некоторого внутреннего блока с незначительной вероятностью.) Тем не менее, мы доказали, что OMAC является таким же защищённым как и XCBC, где анализ безопасности является образцом абсолютной защищённости. Дальнейший OMAC получил все другие положительные свойства, которыми были наделены XCBC. Таким образом, область OMAC — {0,1}, необходимо одноключевое расписание базового блочного шифра E и блочно-шифровых вызовов.