Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Быстрые криптосистемы с открытым ключом - NTRU23 января 2011Оглавление: 1. Быстрые криптосистемы с открытым ключом 2. NTRU 3. Криптосистема, основанная на группе кос 4. Сравнение NTRU был разработан в середине 1990-х годов и впервые был представлен на конференции CRYPTO’96. NTRU запатентован NTRU Cryptosystems, Inc. 24 июля 2000 года. В этом алгоритме все операции производятся в кольце усечённых многочленов. Криптографическая стойкость алгоритма основана на сложности задачи нахождения короткого вектора в заданной решётке. NTRU работает быстрее, чем используемые в настоящее время криптосистемы с открытым ключом. Для шифрования и расшифрования сообщения длиной N символов необходимо O операций для алгоритма NTRU, в то время как для RSA требуется O операций. Криптографическая стойкость NTRU ещё не достаточно исследована. Кроме того NTRU является ненадёжным алгоритмом, то есть при расшифровании можно получить сообщение, отличающее от того, которое использовалось при шифровании. Криптостойкость NTRU-167 примерно соответствует RSA-512. Стойкость NTRU-263 и NTRU-503 сопоставима со стойкостью RSA-1024 и RSA-2048 соответственно. При этом при использовании NTRU-263 длина открытого ключа равняется 1841 биту, а секретного — 834 бита. В NTRU зашифрованное сообщение больше открытого текста примерно в 4,5 раза. Кольцо усечённых многочленовРазличные реализации NTRU характеризуются тремя целыми числами — N, p и q. Числа p и q не обязательно должны быть простыми, но необходимо, чтобы они не имели общих делителей. Базовыми объектами в NTRU являются многочлены порядка N-1 с целочисленными коэффициентами:
Операция сложения определена просто, как сложение коэффициентов при соответствующих степенях:
Операция умножения определена так же, с помощью умножения коэффициентов при соответствующих степенях, с одной поправкой. При умножении многочленов X необходимо заменить на 1, X заменить на X и т. д.:
Правила сложения и умножения обладают свойством дистрибутивности:
Кольцо многочленов с определёнными таким образом операциями сложения и умножения называется кольцом усечённых многочленов. Оно изоморфно кольцу отношений Z /. В NTRU используются кольца усечённых многочленов с арифметикой по модулю p и q. Это значит, что коэффициенты ai и bi складываются и умножаются по модулю. Генерация ключаПусть R — кольцо усечённых многочленов. Если Боб хочет создать пару ключей, он случайно выбирает многочлены
Секретным ключом будет пара f, ШифрованиеЕсли Алиса хочет отправить сообщение Бобу, используя его открытый ключ h, ей необходимо представить сообщение в виде многочлена m, коэффициенты которого взяты по модулю p. Также ей необходимо произвольно выбрать многочлен r. Далее, используя эти параметры, она вычисляет многочлен
Многочлен e является зашифрованным сообщением, которое хочет отправить Алиса. РасшифрованиеПредположим Боб получил зашифрованное сообщение, которое послала ему Алиса. Для начала ему необходимо вычислить
используя известный только ему многочлен f. Теперь Боб может восстановить сообщение Алисы, вычислив
Как это работаетРассмотрим почему при расшифровании получается исходное сообщение:
Следует заметить, что при расшифровании может получиться сообщение отличающееся от исходного. Это происходит из-за того, что операции произоводятся сначала по модулю q, а потом по модулю p. На практике, если правильно выбрать параметры, вероятность возникновения такой ошибки становится меньше, чем 2 . Просмотров: 6331
|
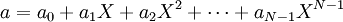 .
.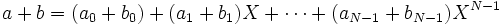 .
.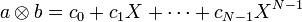 , где
, где 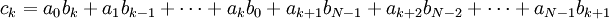 .
.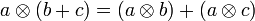 .
.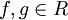 . Многочлен f должен иметь обратный многочлен по модулю p и q. Если для f не существует обратного, то Боб должен выбрать другой многочлен. Далее Боб должен вычислить обратные многочлены по модулю p и q, обозначим их
. Многочлен f должен иметь обратный многочлен по модулю p и q. Если для f не существует обратного, то Боб должен выбрать другой многочлен. Далее Боб должен вычислить обратные многочлены по модулю p и q, обозначим их 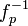 и
и 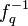 соответственно. Затем нужно вычислить
соответственно. Затем нужно вычислить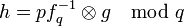 .
.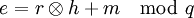 .
.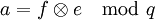 ,
,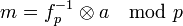 .
.