Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Быстрая цифровая подпись - Некоторые алгоритмы быстрой цифровой подписи22 января 2011Оглавление: 1. Быстрая цифровая подпись 2. Некоторые алгоритмы быстрой цифровой подписи 3. Применение быстрой ЭЦП. Схема быстрой ЭЦП, основанная на алгоритме Диффи-ХеллманаПусть Генерация ключа Пользователь выбирает случайный секретный ключ Создание подписи Входными данными являются секретный ключ Далее сторона, создающая подпись: 1. выбирает случайное число 2. вычисляет 3. вычисляет 4. вычисляет 5. вычисляет 6. вычисляет Подписью сообщения Проверка подписи Чтобы проверить подпись 1. 2. вычисляется 3. вычисляется 4. проверяется, выполняется ли Если равенство на шаге 4 выполняется, подпись проходит проверку. Схема быстрой ЭЦП, основанная на алгоритме Фиата-ШамираZN обозначает кольцо целых чисел по модулю Роль центра аутентификации ключей ЦАК выбирает:
КАЦ публикует Секретный ключ ЦАК используется для подписи создаваемых им открытых ключей. Для создания таких подписей ЦАК может использовать любую безопасную схему ЭЦП. Генерация пользовательских ключей. Каждый пользователь выбирает секретный ключ Регистрация пользователей. ЦАК проверяет соответствие пользователя, создает строку Создание подписи. Входное сообщение 1. Выбирается случайное число 2. Вычисляется 3. Вычисляется Подписью на выходе является пара Создание подписи требует не более Проверка подписи. Входные данные — подпись 1. Проверяется подпись 2. Вычисляется 3. Проверяется, что Для проверки подписи требуется в среднем для случайного Безопасность подписи. Чтобы подделать подпись сообщения В настоящее время неизвестно алгоритмов для решения этого уравнения. Просмотров: 2461
|
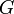 – абелева группа,
– абелева группа, 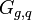 – её циклическая подгруппа с генератором
– её циклическая подгруппа с генератором 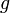 порядка
порядка 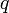 , где
, где 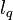 и
и 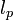 - параметры безопасности, причем
- параметры безопасности, причем 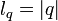 . Пусть
. Пусть 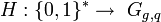 ,
, 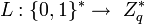 и
и 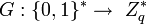 - хэш-функции. Схема подписи представляет из себя следующее:
- хэш-функции. Схема подписи представляет из себя следующее: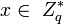 и вычисляет открытый ключ y = g.
и вычисляет открытый ключ y = g.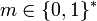 .
.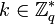 и случайный бит
и случайный бит 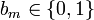 ;
;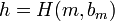 ;
;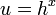 ;
;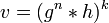 , где
, где 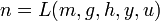 ;
;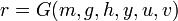 ;
;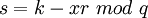 .
.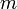 является
является 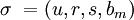 .
.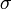 сообщения m, делается следующее:
сообщения m, делается следующее: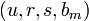 ;
;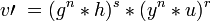 ;
;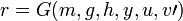 .
.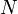 ,
, 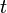 и
и 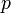 — параметры безопасности, обычно
— параметры безопасности, обычно 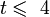 ,
, 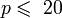
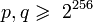 ;
;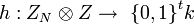 ;
;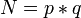 ,
, 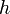 и открытый ключ.
и открытый ключ.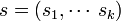 , состоящий из случайных чисел
, состоящий из случайных чисел  ,
, 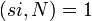 для всех
для всех  от 1 до
от 1 до 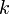 . Создание подписи может быть ускорено, если выбирать в качестве
. Создание подписи может быть ускорено, если выбирать в качестве 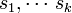 небольшие целые числа. Безопасность такой схемы основана на предположении о том, что вычисление корней
небольшие целые числа. Безопасность такой схемы основана на предположении о том, что вычисление корней 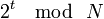 является трудным. В настоящее время неизвестно о существовании алгоритмов, вычисляющих корни
является трудным. В настоящее время неизвестно о существовании алгоритмов, вычисляющих корни 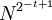 .
.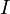 , содержащую имя, адрес и т. д. и создает подпись
, содержащую имя, адрес и т. д. и создает подпись 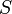 для пары
для пары 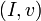 , состоящую из
, состоящую из 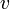 .
. из диапазона
из диапазона 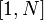 , вычисляется
, вычисляется 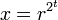 .
.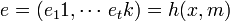 .
.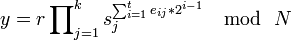 .
.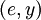 .
.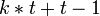 операций умножения по модулю, а в среднем для случайного
операций умножения по модулю, а в среднем для случайного  требуется только
требуется только 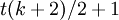 операций умножения.
операций умножения.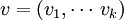 ,
, 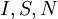 .
.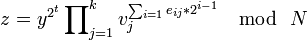 .
.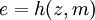 .
.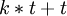 .
.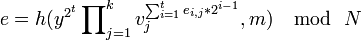 для
для 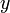 .
.