Билинейная интерполяция

Интернет магазин китайских планшетных компьютеров

Компьютеры - Билинейная интерполяция

22 января 2011
Вип-сувениры с логотипом: сувенирная продукция с логотипом www.alfagrafika.ru.

Оглавление:
1. Билинейная интерполяция
2. Билинейная интерполяция в компьютерной графике
3. Пример программы

в вычислительной математике расширение линейной интерполяции для функций двух переменных. Ключевая идея заключается в том, чтобы провести обычную линейную интерполяцию сначала в одном направлении, затем в другом.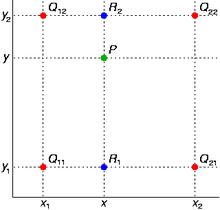

Четыре красные точки представляют собой известные значения функции. Значение в зеленой точке должно быть интерполировано.

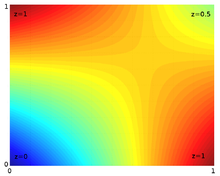
Пример билинейной интерполяции в единичном квадрате. Значения вершин составляют 0, 1, 1 и 0.5. Интерполированные значения в каждой точке представлены цветом.

Допустим, что необходимо интерполировать значение функции f в точке P =. Для этого необходимо знать значения функций в точках Q₁₁ =, Q₁₂ =, Q₂₁ =, и Q₂₂ =.

Первым шагом интерполируется значение вспомогательных точек R₁ и R₂ вдоль оси абсцисс, где

R₁ =

R₂ =

$f \approx \frac{x_2-x}{x_2-x_1} f + \frac{x-x_1}{x_2-x_1} f$

Теперь проводится линейная интерполяция между вспомогательными точками R₁ и R₂.

$f \approx \frac{y_2-y}{y_2-y_1} f + \frac{y-y_1}{y_2-y_1} f.$

Это и есть приблизительное значение функции в точке P, то есть f.

$\begin{align} f &\approx \frac{f}{} \\ & + \frac{f}{} \\ & + \frac{f}{} \\ & + \frac{f}{}. \end{align}$

В особом случае, когда известные точки находятся на вершинах единичного квадрата, то есть имеют координаты,,, и, формула билинейной интерполяции упрощается до

$f \approx f \, + f \, x + f \,y + f xy.$

Или же с помощью умножения векторов с матрицей:

$f \approx \begin{bmatrix} 1-x & x \end{bmatrix} \begin{bmatrix} f & f \\ f & f \end{bmatrix} \begin{bmatrix} 1-y \\ y \end{bmatrix}$

Обратите внимание: сам интерполянт нелинеен:

$, \,$

так как является произведением двух линейных функций. Альтернативное написание:

$b_1 + b_2 x + b_3 y + b_4 x y \,$

где

$b_1 = f \,$

$b_2 = f-f \,$

$b_3 = f-f \,$

$b_4 = f-f-f+f \,$ .

Результат билинейной интерполяции не зависит от порядка шагов. Возможно сначала интерполировать между известными точками вдоль оси ординат и затем, получив два вспомогательных значения, интерполировать между ними вдоль оси абсцисс. Результат будет тот же.

Очевидное расширение билинейной интерполяции на функции трех переменных — трилинейная интерполяция.

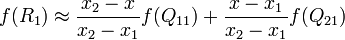
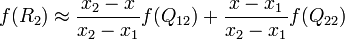
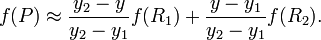
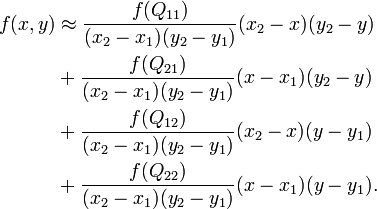
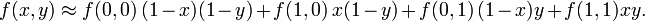
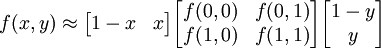
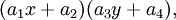
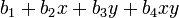
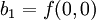
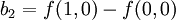
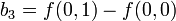
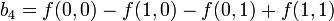<<< Алгоритмы построения отрезка

Графический метод решения задачи линейного программирования >>>

Компьютерное аппаратное обеспечение
Вычислительные комплексы
Компьютерные данные
Компьютерные журналы
Классы компьютеров
Компьютеры

Программное обеспечение
Производители компьютеров
Профессии в ИТ
Системное администрирование
Компьютерный сленг
Списки компьютерных терминов

Человеко-компьютерное взаимодействие