Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Бикубическая интерполяция - Бикубическая интерполяция сплайнами22 января 2011Оглавление: 1. Бикубическая интерполяция 2. Бикубическая интерполяция сплайнами Допустим, что необходимо интерполировать значение функции f в точке P, лежащей внутри квадрата Для нахождения коэффициентов aij необходимо подставить в вышеприведенное уравнение значения функции в известных шестнадцати точках. Например:
Полностью в матричном виде: Mα = γ, где
Решая получившуюся систему линейных алгебраических уравнений, можно найти значения aij в явном виде:
Единожды найденные коэффициенты aij теперь могут быть использованы для многократного вычисления интерполированного значения функции в произвольных точках квадрата Последовательная кубическая интерполяцияДругая интерпретация метода заключается в том, что для нахождения интерполированного значения можно сначала произвести кубическую интерполяцию в одном направлении, а затем в другом. Для функции f с известными значениями f, f, f, f можно построить кубический сплайн:
где
Таким образом, для нахождения интерполированного значения p в квадрате
Просмотров: 3345
|
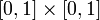 , и известно значение функции f в шестнадцати соседних точках
, и известно значение функции f в шестнадцати соседних точках 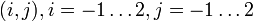 . Тогда общий вид функции, задающей интерполированную поверхность, может быть записан следующим образом:
. Тогда общий вид функции, задающей интерполированную поверхность, может быть записан следующим образом: 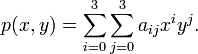
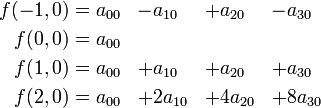 .
.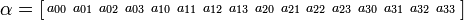 ,
,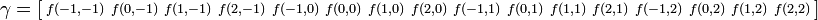 ,
,![M=\left[\begin{smallmatrix}
1 & -1 & 1 & -1 & -1 & 1 & -1 & 1 & 1 & -1 & 1 & -1 & -1 & 1 & -1 & 1 \\
1 & -1 & 1 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\
1 & -1 & 1 & -1 & 2 & -2 & 2 & -2 & 4 & -4 & 4 & -4 & 8 & -8 & 8 & -8 \\
1 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & -1 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 2 & 0 & 0 & 0 & 4 & 0 & 0 & 0 & 8 & 0 & 0 & 0 \\
1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 & 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 \\
1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
1 & 1 & 1 & 1 & 2 & 2 & 2 & 2 & 4 & 4 & 4 & 4 & 8 & 8 & 8 & 8 \\
1 & 2 & 4 & 8 & -1 & -2 & -4 & -8 & 1 & 2 & 4 & 8 & -1 & -2 & -4 & -8 \\
1 & 2 & 4 & 8 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
1 & 2 & 4 & 8 & 1 & 2 & 4 & 8 & 1 & 2 & 4 & 8 & 1 & 2 & 4 & 8 \\
1 & 2 & 4 & 8 & 2 & 4 & 8 & 16 & 4 & 8 & 16 & 32 & 8 & 16 & 32 & 64
\end{smallmatrix}\right]](/c/img/7589.png) .
.![\alpha^T = \frac{1}{36}\left[\begin{smallmatrix}
0 & 0 & 0 & 0 & 0 & 36 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & -12 & 0 & 0 & 0 & -18 & 0 & 0 & 0 & 36 & 0 & 0 & 0 & -6 & 0 & 0 \\
0 & 18 & 0 & 0 & 0 & -36 & 0 & 0 & 0 & 18 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & -6 & 0 & 0 & 0 & 18 & 0 & 0 & 0 & -18 & 0 & 0 & 0 & 6 & 0 & 0 \\
0 & 0 & 0 & 0 & -12 & -18 & 36 & -6 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
4 & 6 & -12 & 2 & 6 & 9 & -18 & 3 & -12 & -18 & 36 & -6 & 2 & 3 & -6 & 1 \\
-6 & -9 & 18 & -3 & 12 & 18 & -36 & 6 & -6 & -9 & 18 & -3 & 0 & 0 & 0 & 0 \\
2 & 3 & -6 & 1 & -6 & -9 & 18 & -3 & 6 & 9 & -18 & 3 & -2 & -3 & 6 & -1 \\
0 & 0 & 0 & 0 & 18 & -36 & 18 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
-6 & 12 & -6 & 0 & -9 & 18 & -9 & 0 & 18 & -36 & 18 & 0 & -3 & 6 & -3 & 0 \\
9 & -18 & 9 & 0 & -18 & 36 & -18 & 0 & 9 & -18 & 9 & 0 & 0 & 0 & 0 & 0 \\
-3 & 6 & -3 & 0 & 9 & -18 & 9 & 0 & -9 & 18 & -9 & 0 & 3 & -6 & 3 & 0 \\
0 & 0 & 0 & 0 & -6 & 18 & -18 & 6 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
2 & -6 & 6 & -2 & 3 & -9 & 9 & -3 & -6 & 18 & -18 & 6 & 1 & -3 & 3 & -1 \\
-3 & 9 & -9 & 3 & 6 & -18 & 18 & -6 & -3 & 9 & -9 & 3 & 0 & 0 & 0 & 0 \\
1 & -3 & 3 & -1 & -3 & 9 & -9 & 3 & 3 & -9 & 9 & -3 & -1 & 3 & -3 & 1 \\
\end{smallmatrix}\right] x^T](/c/img/7590.png) .
.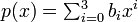 , или в матричном виде
, или в матричном виде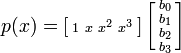 ,
,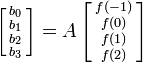 ,
,![A =
\frac{1}{6}
\left[\begin{smallmatrix}
0 & 6 & 0 & 0\\
-2 & -3 & 6 & -1\\
3 & -6 & 3 & 0\\
-1 & 3 & -3 & 1
\end{smallmatrix}\right]](/c/img/7594.png) .
.![p =
\left A
\left(
\left A
\left[\begin{smallmatrix}
& f & f & f & f \\
& f & f & f & f \\
& f & f & f & f \\
& f & f & f & f \\
\end{smallmatrix}\right]
\right)^T
=](/c/img/7595.png)
![=
\left A
\left[\begin{smallmatrix}
f & f & f & f \\
f & f & f & f \\
f & f & f & f \\
f & f & f & f
\end{smallmatrix}\right]
A^T
\left[\begin{smallmatrix}
1 \\ x \\ x^2 \\ x^3
\end{smallmatrix}\right]](/c/img/7596.png)