Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Арифметико-логический способ представления троичных функций - Преобразование троичных функций23 января 2011Оглавление: 1. Арифметико-логический способ представления троичных функций 2. Преобразование троичных функций 3. Функциональная полнота арифметико-логического способа представления троичных функций элементов 4. Представление основных троичных функций арифметико-логическим способом Для преобразования и минимизации троичных функций, представленных указанным способом, можно использовать следующие тождества. Отметим, что k, k1,k2,k ∈ {-1,0,1} и k1≠k1≠k3: Эти тождества доказываются прямой проверкой. Тождества и функции f1 и f2 могут преобразоваться и минимизироваться с использованием тождеств и законов двоичной логики, так как их аргументы являются двухзначными функциями . Например, если справедливо тождество № 6, то справедливо и равенство Важным является равенство-=f1²-f2², которое справедливо в том случае, когда двоичная функция f² приобретает единичное значение на наборах аргументов, на которых функции f1² и f2² приобретают нулевое значение. Равенство базируется на использовании того факта, что разница 1-1 равняется 0. Пусть f — двоичная функция некоторого логического элемента. Тогда, функция f³ соответствующего ~ элемента, может быть представлена в виде произведения трёхзначной функции на двоичную, то есть: Воспользуемся формулой Начальная функция Для примера преобразования троичных функций покажем, как от последнего представления функции ~И-НЕ перейти к приведенному выше её виду. На основе распределительного закона: 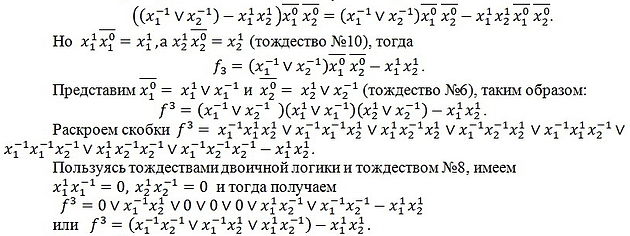 Таким образом, путём преобразований доказывается эквивалентность двух приведенных аналитических видов функций ~ И-НЕ. Просмотров: 4304
|
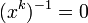
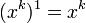
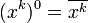
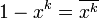
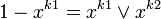
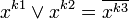
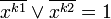
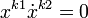
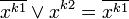
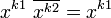
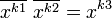
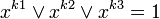
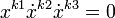
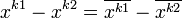
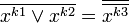 . Или на основе правил де-Моргана и двойного отрицания получим
. Или на основе правил де-Моргана и двойного отрицания получим 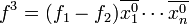 . Отметим, что для этого формулу функции f необходимо представлять в дизъюнктивной нормальной форме, конъюнктивной нормальной форме или в форме со скобками. Функция f1 строится только по ДНФ, КНФ или по форме начальной функции f заменой xi на xi и
. Отметим, что для этого формулу функции f необходимо представлять в дизъюнктивной нормальной форме, конъюнктивной нормальной форме или в форме со скобками. Функция f1 строится только по ДНФ, КНФ или по форме начальной функции f заменой xi на xi и 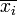 на xi. Функция f2 строится по ДНФ, КНФ или в форме со скобками, но только по инверсии функции f .
на xi. Функция f2 строится по ДНФ, КНФ или в форме со скобками, но только по инверсии функции f .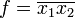 . Её ДНФ —
. Её ДНФ — 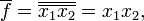 таким образом, f2=x1x2. А значит, имеем
таким образом, f2=x1x2. А значит, имеем