Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Алгоритм Гровера23 января 2011Оглавление: 1. Алгоритм Гровера 2. Алгоритмы, использующие схему Гровера 3. Применение Алгоритм Гровера GSA — быстрый квантовый алгоритм решения задачи перебора, то есть нахождения решения уравнения GSA находит какой-нибудь корень уравнения, используя Если уравнение имеет l корней, по схеме Гровера можно найти один из них на квантовом компьютере за время Классический алгоритм решения такой задачи, очевидно требует 1). Константу 2). Большего квантового ускорения, чем квадратичное, нельзя получить для неисчезающей доли всех возможных черных ящиков f . GSA есть пример массовой задачи, зависящей от оракула. Для более частных задач удается получить большее квантовое ускорение. Например, алгоритм факторизации Шора, дает экспоненциальный выигрыш по сравнению с соответствующими классическими алгоритмами. То что f задана в виде черного ящика, никак не влияет в общем случае на сложность как квантовых, так и классических алгоритмов. Знание «устройства» функции f в общем случае никак не может помочь в решении уравнения. Поиск в базе данных соотносится с обращением функции, которая принимает определенное значение, если аргумент x соответствует искомой записи в базе данных. Пусть Ia есть унитарный оператор, зеркально отражающий гильбертово пространство относительно гиперплоскости, перпендикулярной вектору a,
Просмотров: 3197
|
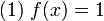 где f есть булева функция от n переменных.. Предполагается, что функция f задана в виде черного ящика, или оракула, то есть в ходе решения мы можем только задавать оракулу вопрос типа: «чему равна f на данном x», и после получения ответа использовать его в дальнейших вычислениях). То есть задача решения уравнения является общей формой задачи перебора; здесь требуется отыскать «пароль к устройству f», что классически требует прямого перебора всех N = 2 вариантов.
где f есть булева функция от n переменных.. Предполагается, что функция f задана в виде черного ящика, или оракула, то есть в ходе решения мы можем только задавать оракулу вопрос типа: «чему равна f на данном x», и после получения ответа использовать его в дальнейших вычислениях). То есть задача решения уравнения является общей формой задачи перебора; здесь требуется отыскать «пароль к устройству f», что классически требует прямого перебора всех N = 2 вариантов.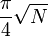 обращений к функции f, с использованием O кубитов.. Алгоритм был открыт американским математиков Ловом Гровером в 1996 году.
обращений к функции f, с использованием O кубитов.. Алгоритм был открыт американским математиков Ловом Гровером в 1996 году.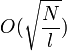 , то есть снова квантовая сложность является квадратным корнем из классической.
, то есть снова квантовая сложность является квадратным корнем из классической.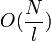 обращений к f. Алгоритм Гровера позволяет решить задачу поиска за время порядка квадратного корня из классического, что является огромным ускорением. Доказано, что GSA является оптимальным в следующих отношениях.
обращений к f. Алгоритм Гровера позволяет решить задачу поиска за время порядка квадратного корня из классического, что является огромным ускорением. Доказано, что GSA является оптимальным в следующих отношениях.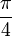 нельзя улучшить более чем на 3 % .
нельзя улучшить более чем на 3 % .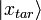 — есть состояние, соответствующее корню уравнения,
— есть состояние, соответствующее корню уравнения, 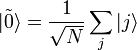 — равномерная суперпозиция всех состояний. Тогда GSA состоит в применении оператора
— равномерная суперпозиция всех состояний. Тогда GSA состоит в применении оператора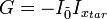 к состоянию
к состоянию 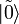 число раз, равное целой части
число раз, равное целой части 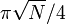 . Результат будет почти совпадать с состоянием
. Результат будет почти совпадать с состоянием