Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Алгоритм Гилберта Джонсона Кёрти - Описание23 января 2011Оглавление: 1. Алгоритм Гилберта Джонсона Кёрти 2. Описание 3. Использование Алгоритм Гилберта — Джонсона — Кёрти предоставляет довольно эффективный метод обнаружения столкновений между выпуклыми объектами. Он полагается на несколько ключевых моментов, которые кратко выделены ниже: Сумма Минковского: Имеется два множества A и B, их сумма Минковского определяется как: Это определение кажется неправильным, так как суммирование точек бессмысленно. В этом свободном замечании x и y пусть скорее будут восприняты как векторы Конфигурационное пространство препятствий. Для пары Кроме того, их дистанция даётся: Подобным образом глубина проникновения пар объектов может быть выраженная в терминах их CSO как: Для пары пересекающихся объектов глубина проникновения реализуется точкой на границе A − B, которая наиболее близка к началу системы координат. Support Mapping. Support Mapping SA является функцией, которая принимает вектор v и выпуклое множество A, возвращает наиболее «экстремальную» точку для выпуклого объекта A в этом направлении. Формально говоря: Разделяющая плоскость/ось: Дано два объекта A и B, плоскость Общая идея алгоритма GJK состоит в изучении конфигурационного пространства препятствий для двух данных объектов A и B, ища симплекс, который содержит начало системы координат. Если поиск заканчивается с отрицательным ответом, то есть начало системы координат лежит вне CSO, то тогда объекты не пересекаются. В этом случае точка из CSO, которая является ближайшей к началу системы координат, представляет разделяющую ось A и B, и это, в свою очередь, может использоваться как отправная точка для тестирования столкновений в последующих итерациях. 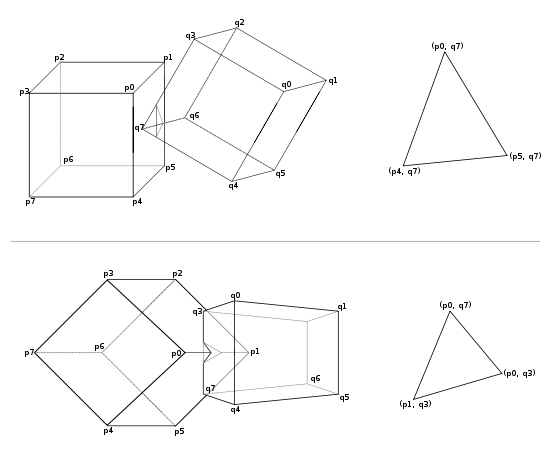
Два типа столкновений и соответствующих им CSO-граней: грань-вершина и ребро-ребро
С другой стороны, если поиск был успешен, и потом объекты пересеклись, то для того, чтобы исполнить реакцию на столкновение и некоторые другие детали по отношению к столкновению, необходимы вычисления. Например, типичная схема, пытающаяся определить глубину проникновения, которая, в свою очередь, нуждается в поиске точки на границе CSO, которая будет ближайшей к началу системы координат. Ван ден Берген предлагает расширенный алгоритм политопов для этого случая. Однако наша система вычисляет относительную информацию — ударную грань, то есть ту грань на оболочке CSO, которая является ближайшей к началу системы координат. Анализируя вершины в этой грани, является возможным определить, какая составная часть объекта приняла участие в столкновении. Здесь различают два основных случая: столкновения типа «ребро-ребро» и столкновения типа «вершина-грань». Для того, чтобы понять, как идентифицируются составные части, заметим, что каждый из CSO соответствует паре векторов Просмотров: 3654
|
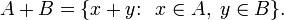
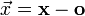 , где
, где 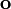 является началом мировой системы координат.
является началом мировой системы координат.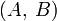 выпуклых объектов их CSO будет дано A − B, то есть сумма Минковского от A и − B. Этот набор особенно полезный в определениях столкновений, так как он может доказать, что A и B пересекаются тогда и только тогда, когда их CSO содержат начало системы координат:
выпуклых объектов их CSO будет дано A − B, то есть сумма Минковского от A и − B. Этот набор особенно полезный в определениях столкновений, так как он может доказать, что A и B пересекаются тогда и только тогда, когда их CSO содержат начало системы координат: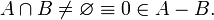
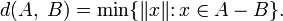
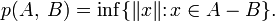
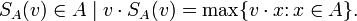
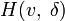 , которая разделяет A и B, если для каждой точки
, которая разделяет A и B, если для каждой точки 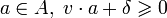 и для каждой точки
и для каждой точки 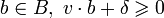 . Вектор v известен как «слабо отделённая ось» для A и B, поскольку есть по крайней мере одна отделяющая плоскость, которая есть нормалью к нему, или, эквивалентно,
. Вектор v известен как «слабо отделённая ось» для A и B, поскольку есть по крайней мере одна отделяющая плоскость, которая есть нормалью к нему, или, эквивалентно,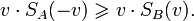
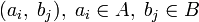 . Например, вершина выпуклого объекта A столкнулась с гранью выпуклого объекта B, которая характеризуется тем, что имеет все три вершины ударной грани, соответственные к той самой вершине объекта A, но к трём разным вершинам объекта B.
. Например, вершина выпуклого объекта A столкнулась с гранью выпуклого объекта B, которая характеризуется тем, что имеет все три вершины ударной грани, соответственные к той самой вершине объекта A, но к трём разным вершинам объекта B.