Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Алгоритм Джарвиса23 января 2011Оглавление: 1. Алгоритм Джарвиса 2. Анализ Алгоритм Джарвиса определяет последовательность элементов множества, образующих выпуклую оболочку для этого множества. Метод можно представить как обтягивание верёвкой множества вбитых в доску гвоздей. Алгоритм работает за время O, где n — общее число точек на плоскости, h — число точек в выпуклой оболочке. 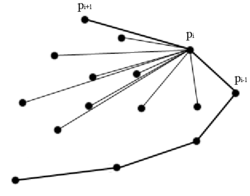
Алгоритм Джарвиса построения выпуклой оболочки
Описание алгоритмаПусть дано множество P = {p1,p2,...pn} точек. В качестве начальной берётся самая левая нижняя точка p1 обычным проходом по всем точкам), она точно является вершиной выпуклой оболочки. Затем для каждой точки pi ищется против часовой стрелки точка pi + 1 путём нахождения за O среди оставшихся точек точки с наименьшим полярным углом pi − 1pipi + 1. Она и будет следующей вершиной выпуклой оболочки. При этом сам угол не обязательно вычислять, достаточно вычислить векторное произведение между лучами pip'i + 1 и pip''i + 1, где p'i + 1 найденный на данный момент минимум, p''i + 1 претендент. Если векторное произведение отрицательно, то найден новый минимум. Если равно нулю, то есть p'i + 1 и p''i + 1 лежат на одной прямой, то минимум та, которая лежит дальше от точи pi. Алгоритм продолжается пока
Jarvis
1) p = самая левая нижняя точка множества P;
2) i = 1;
3) do:
p = любая точка из P;
for
p = min_polar_angle; // минимум через векторное произведение, как описано выше
i = i + 1;
while p != p
4) return p;
Просмотров: 4023
|
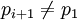 . Почему алгоритм остановится? Потому что самая левая нижняя точка в любом случае принадлежит выпуклой оболочке.
. Почему алгоритм остановится? Потому что самая левая нижняя точка в любом случае принадлежит выпуклой оболочке.