Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Алгоритм де Кастельжо - Геометрическая интерпретация23 января 2011Оглавление: 1. Алгоритм де Кастельжо 2. Геометрическая интерпретация Геометрическая интерпретация алгоритма де Кастельжо проста:
Следующая иллюстрация демонстрирует этот процесс для кубической кривой Безье:
Следует заметить, что полученные в процессе построения промежуточные точки являются опорными точками для двух новых кривых Безье, в точности совпадающих с исходной, и в совокупности дающих исходную кривую Безье. Этот алгоритм не только определяет точку кривой в Описанный алгоритм справедлив для нерациональных кривых Безье. Для вычисления рациональных кривых в В целом, операции с рациональными кривыми эквивалентны операциям с нерационалиными кривыми в проективном пространстве. Представление опорных точек как взвешенных часто бывает удобно для определения рациональных кривых. Просмотров: 5254
|
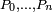 . Соединив последовательно опорные точки с первой по последнюю, получаем ломаную линию.
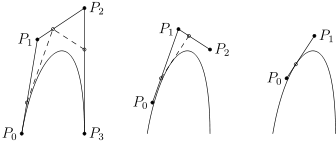
. Соединив последовательно опорные точки с первой по последнюю, получаем ломаную линию.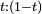 и соединяем полученные точки. В результате получаем ломаную линию с количеством отрезков, меньшим на один, чем исходная ломаная линия.
и соединяем полученные точки. В результате получаем ломаную линию с количеством отрезков, меньшим на один, чем исходная ломаная линия. .
.
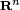 , можно спроецировать точку в
, можно спроецировать точку в 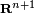 ; например кривая в трехмерном пространстве должна иметь опорные точки
; например кривая в трехмерном пространстве должна иметь опорные точки 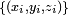 и веса
и веса 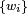 спроецированные в весовые контрольные точки
спроецированные в весовые контрольные точки 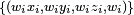 . Затем обычно алгоритм переходит к интерполяции в
. Затем обычно алгоритм переходит к интерполяции в 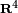 . Результирующие четырехмерные точки могут быть спроецированы обратно в трехмерное пространство с помощью перспективного деления.
. Результирующие четырехмерные точки могут быть спроецированы обратно в трехмерное пространство с помощью перспективного деления.