Интернет магазин китайских планшетных компьютеров

Компьютеры - Алгоритм Чана - Выбор числа точек m

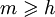Ясно, что обход по Джарвису, а следовательно и весь алгоритм, будет корректно работать только если , но как заранее узнать сколько точек будет в выпуклой оболочке? Надо запускать алгоритм несколько раз, подбирая m и, если m < h, то алгоритм будет возвращать ошибку. Если делать подбор бинарным поиском по n, то в итоге получится время Ologn) = O, что достаточно долго.

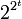Процесс можно ускорить, если начать с маленького значения и после значительно его увеличивать, пока не получится . Например, взять . При этом t-я итерация займет 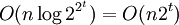. Процесс поиска завершится, когда 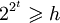, то есть .

В итоге .

ChanHull
 for t = 1 to n do:
     взять ;
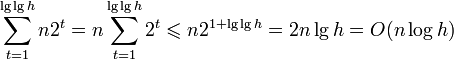     L = Hull;
     if L != «m маленькое, попробуйте еще» return L;