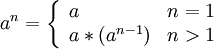Интернет магазин китайских планшетных компьютеров

Компьютеры - Алгоритм быстрого возведения в степень - Оценка сложности

Чтобы узнать, сколько умножений потребуется для возведения числа x в степень n алгоритмом быстрого возведения в степень, нужно произвести вычисления по следующей формуле: k = H + 2, где H — количество нулей, а E — количество единиц в двоичной записи числа n.

Так, для возведения числа в сотую степень этим алгоритмом потребуется всего лишь 8 умножений.

Таким образом количество умножений равно O.

Обобщение

Пусть пара — полугруппа, то есть S — произвольное множество, на котором задана бинарная операция * такая, что:

• Для любых элементов a и b из S справедливо: так же из S.
• Для любых элементов a, b и c из S справедливо: * c) =).

Мы можем назвать операцию * умножением и определить операцию возведения в натуральную степень:

Для вычисления значений a можно использовать алгоритм быстрого возведения в степень.