Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Алгоритм быстрого возведения в степень22 января 2011Оглавление: 1. Алгоритм быстрого возведения в степень 2. Оценка сложности алгоритм, предназначенный для возведения числа x в натуральную степень n за меньшее число умножений, чем это требуется в определении. Алгоритм не всегда оптимален. Например, при n=15 требуется 6 умножений, хотя на самом деле возведение в 15-ую степень можно выполнить за 5 умножений. Теоретические основы алгоритмаПусть Таким образом, алгоритм быстрого возведения в степень сводится к мультипликативному аналогу схемы Горнера.
Программная реализацияИспользуется представление числа x:
Язык Си
int power // возведение t в степень k
{
int res = 1;
while
{
if
res *= t;
t *= t;
k >>= 1;
}
return res;
}
Delphi
function Power: NativeInt; inline;
begin
Result := 1;
while true do
begin
if Odd then
Result := Result * t;
k := k shr 1;
if k = 0 then
break;
t := t * t;
end;
end;
Паскаль
function power: integer; {возведение числа t в степень k}
var
res:integer;
begin
res := 1;
while true do
begin
if k mod 2 = 1 then {или напишите "if Odd then" для большей скорости выполнения}
res := res * t;
k := k div 2; {или напишите "k := k shr 1;" для большей скорости выполнения}
if k = 0 then
break;
t := t * t; {или напишите "t:= sqr;" для большей скорости выполнения}
end;
power := res;
end;
Python
def FastPow : # Быстрое возведение числа t в степень k
res = 1
while k:
if :
res *= t
k = k >> 1
if k == 0:
break
t *= t
return res
Просмотров: 4881
|
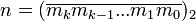 — двоичное представление степени n. Тогда
— двоичное представление степени n. Тогда 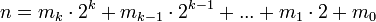 , где
, где 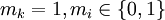 и
и 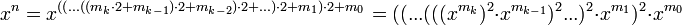 .
.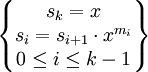
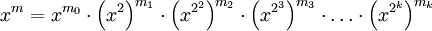 .
.