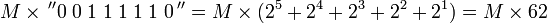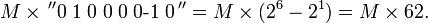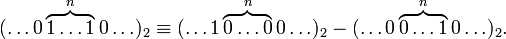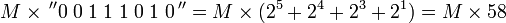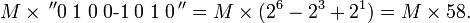Интернет магазин китайских планшетных компьютеров

Компьютеры - Алгоритм Бута - Как это работает

Рассмотрим положительный множитель, состоящий из блока единиц, окруженных нулями, например 00111110. Произведение определяется по формуле :

где M — множимое. Количество операций может быть уменьшено вдвое, если представить произведение слеюущим образом :

На самом деле, можно показать, что любая последовательность единиц в двоичном числе может быть разбита на разность двух двоичных чисел:

Таким образом, мы действительно можем заменить операцию умножения на последовательность единиц в исходном числе более простыми операциями: сложение с множителем, сдвиг частичного произведения, вычитание множителя. Алгоритм использует тот факт, что нам не нужно делать ничего кроме сдвига, когда очередной разряд в двоичном множителе равен нулю, а также простое математическое свойство: 99 = 100 − 1 при умножении на 99.

Эта схема может быть распространена на любое количество блоков единиц в множителе. Таким образом,

Алгоритм Бута следует этой схеме путем выполнения сложения, когда встречается первая цифра блока единиц, и вычитания, когда встречается конец блока единиц. Схема работает в том числе и для отрицательного множителя. Когда единицы в можителе сгруппированы в длинные блоки, алгоритм Бута выполняет меньше сложений и вычитаний, чем обычный алгоритм умножения.