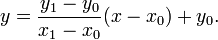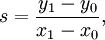Интернет магазин китайских планшетных компьютеров

Компьютеры - Алгоритм Брезенхэма

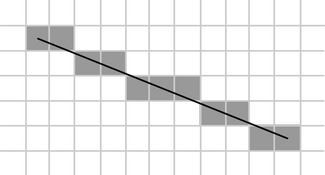
Иллюстрация результата работы алгоритма

Алгоритм Брезенхема — это алгоритм, определяющий, какие точки двумерного растра нужно закрасить, чтобы получить близкое приближение прямой линии между двумя заданными точками. Это один из старейших алгоритмов в машинной графике — он был разработан Джеком Е. Брезенхэмом в компании IBM в 1962 году. Алгоритм широко используется, в частности, для рисования линий на экране компьютера. Существует обобщение алгоритма Брезенхэма для построения кривых 2-го порядка.

Алгоритм

Отрезок проводится между двумя точками — и , где в этих парах указаны колонка и строка, соответственно, номера которых растут вправо и вниз. Сначала мы будем предполагать, что наша линия идёт вниз и вправо, причём горизонтальное расстояние x₁ − x₀ превосходит вертикальное y₁ − y₀, т.е. наклон линии от горизонтали — менее 45°. Наша цель состоит в том, чтобы для каждой колонки x между x₀ и x₁, определить, какая строка y ближе всего к линии, и нарисовать точку .

Общая формула линии между двумя точками:

Поскольку мы знаем колонку x, то строка y получается округлением к целому следующего значения:

Однако, вычислять точное значение этого выражения нет необходимости. Достаточно заметить, что y растёт от y₀ и за каждый шаг мы добавляем к x единицу и добавляем к y значение наклона

которое можно вычислить заранее. Более того, на каждом шаге мы делаем одно из двух: либо сохраняем тот же y, либо увеличиваем его на 1.

Что из этих двух выбрать — можно решить, отслеживая значение ошибки, которое означает — вертикальное расстояние между текущим значением y и точным значением y для текущего x. Всякий раз, когда мы увеличиваем x, мы увеличиваем значение ошибки на величину наклона s, приведённую выше. Если ошибка превысила 0.5, линия стала ближе к следующему y, поэтому мы увеличиваем y на единицу, одновременно уменьшая значение ошибки на 1. В реализации алгоритма, приведённой ниже, plot рисует точку, а abs возвращает абсолютную величину числа:

 function line
     int deltax := abs
     int deltay := abs
     real error := 0
     real deltaerr := deltay / deltax
     int y := y0
     for x from x0 to x1
         plot
         error := error + deltaerr
         if error >= 0.5
             y := y + 1
             error := error - 1.0

Проблема такого подхода — в том, что с вещественными величинами, такими как error и deltaerr, компьютеры работают относительно медленно. Кроме того, при вычислениях с плавающей точкой может накапливаться ошибка. По этим причинам, лучше работать только с целыми числами. Это можно сделать, если умножить все используемые вещественные величины на deltax. Единственная проблема — с константой 0.5 — но в данном случае достаточно умножить обе части неравенства на 2. Получаем следующий код:

 function line
     int deltax := abs
     int deltay := abs
     int error := 0
     int deltaerr := deltay
     int y := y0
     for x from x0 to x1
         plot
         error := error + deltaerr
         if 2 * error >= deltax
             y := y + 1
             error := error - deltax

Умножение на 2 для целых чисел реализуется битовым сдвигом влево.

Теперь мы можем быстро рисовать линии, направленные вправо-вниз с величиной наклона меньше 1. Осталось распространить алгоритм на рисование во всех направлениях. Это достигается за счёт зеркальных отражений, т.е. заменой знака, обменом переменных x и y, обменом координат начала отрезка с координатами конца.