Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Алгоритм Адлемана23 января 2011Оглавление: 1. Алгоритм Адлемана 2. Оценка сложности первый субэкспоненциальный алгоритм дискретного логарифмирования в кольце вычетов по модулю простого числа. Алгоритм был предложен Адлеманом в 1979 году. Исходные данныеПусть задано сравнение
Необходимо найти натуральное число x, удовлетворяющее сравнению. Описание алгоритма1 этап. Сформировать факторную базу, состоящую из всех простых чисел q:
2 этап. С помощью перебора найти натуральные числа ri такие, что
то есть
3 этап. Набрав достаточно много соотношений, решить получившуюся систему линейных уравнений относительно неизвестных дискретных логарифмов элементов факторной базы. 4 этап. С помощью некоторого перебора найти одно начение r, для которого
где 5 этап. С помощью вычислений, аналогичных этапам 2 и 3 найти дискретные логарифмы logapi. 6 этап. Определить искомый дискретный логарифм:
Просмотров: 2006
|
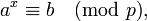
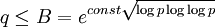
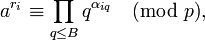
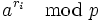 раскладывается по факторной базе. Отсюда следует, что
раскладывается по факторной базе. Отсюда следует, что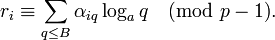
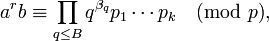
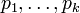 — простые числа «средней» величины, то есть B < pi < B1, где
— простые числа «средней» величины, то есть B < pi < B1, где 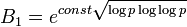 — также некоторая субэкспоненциальная граница.
— также некоторая субэкспоненциальная граница.