Интернет магазин китайских планшетных компьютеров

Компьютеры - Аффинный шифр

Аффинный шифр — это частный случай более общего моноалфавитного шифра подстановки. К шифрам подстановки относятся также шифр Цезаря, ROT13 и Атбаш. Поскольку аффинный шифр легко дешифровать, он обладает слабыми криптографическими свойствами.

Описание

В аффинном шифре каждой букве алфавита размера m ставится в соответствие число из диапазона 0..m − 1. Затем при помощи модульной арифметики для каждого числа, соответствующего букве исходного алфавита, вычисляется новое число, которое заменит старое в шифротексте. Функция шифрования для каждой буквы

где модуль m — размер алфавита, а пара a и b — ключ шифра. Значение a должно быть выбрано таким, что a и m — взаимно простые числа. Функция расшифрования

где a — обратное к a число по модулю m. То есть оно удовлетворяет уравнению

Обратное к a число существует только в том случае, когда a и m — взаимно простые. Значит, при отсутствии ограничений на выбор числа a расшифрование может оказаться невозможным. Покажем, что функция расшифрования является обратной к функции шифрования

Количество возможных ключей для аффинного шифра можно записать через функцию Эйлера как .
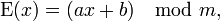
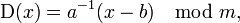
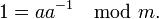
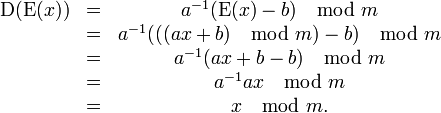
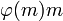