|
|
|
Компьютеры - ACE Encrypt - Схема цифровой подписи30 апреля 2011
Оглавление:
1. ACE Encrypt
2. Безопасность
3. Схема шифрования
4. Схема цифровой подписи
5. Замечания
В схеме цифровой подписи ACE задействованы два типа ключей:
открытый ключ цифровой подписи ACE: 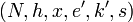 . .
закрытый ключ цифровой подписи ACE: 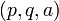 . .
Для заданного параметра размера 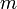 , такого что , такого что 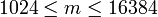 , компоненты ключей определяются следующим образом: , компоненты ключей определяются следующим образом:
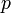 — — 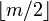 -битное простое число, для которого -битное простое число, для которого 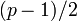 — тоже простое. — тоже простое.
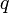 — — 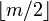 -битное простое число, для которого -битное простое число, для которого 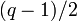 — тоже простое. — тоже простое.
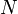 — — 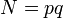 и может иметь как и может иметь как 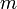 , так и , так и 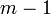 бит. бит.
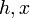 — элементы — элементы 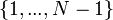 . .
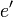 — 161-битное простое число. — 161-битное простое число.
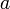 — элемент — элемент 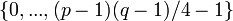
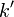 — элементы — элементы 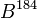 . .
 — элементы — элементы 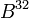 . .
Генерация ключа
Алгоритм. Генерация ключа для схемы цифровой подписи ACE.
Вход: параметра размера 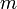 , такой что , такой что 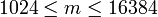 . .
Выход: пара открытый/закрытый ключ.
- Сгенерировать случайные простые числа
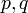 , такие что , такие что 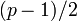 и и 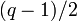 — тоже простые, и — тоже простые, и
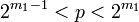 , , 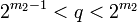 , и , и 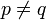 , ,
где
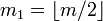 и и 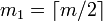 . .
- Положить
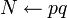 . .
- Сгенерировать случайное простое число
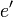 , где , где 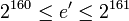 . .
- Сгенерировать случайное
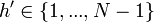 , при условии , при условии 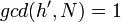 и и 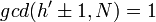 , и вычислить , и вычислить 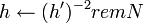 . .
- Сгенерировать случайное
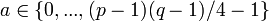 и вычислить и вычислить 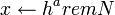 . .
- Сгенерировать случайные байтовые строки
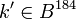 , и , и 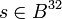 . .
- Вернуть пару открытый ключ/закрытый ключ
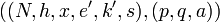 . .
Представление подписи
Подпись в схеме цифровой подписи ACE имеет вид 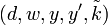 , где компоненты определяются следующим образом: , где компоненты определяются следующим образом:
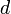 — элемент — элемент 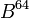 . .
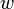 — целое число, такое что — целое число, такое что 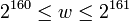 . .
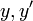 — элементы — элементы 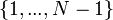 . .
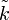 — элемент — элемент 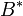 ;заметим, что ;заметим, что 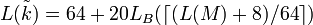 , где , где 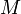 — подписываемое сообщение. — подписываемое сообщение.
Необходимо ввести функцию 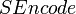 , которая представляет подпись в виде байтовой строки, а также обратную функцию , которая представляет подпись в виде байтовой строки, а также обратную функцию 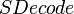 . Для целого . Для целого 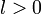 , байтовой строки , байтовой строки 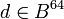 , целых , целых 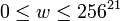 и и 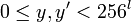 , и байтовой строки , и байтовой строки 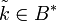 , ,
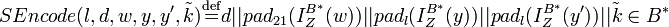 . .
Для целого 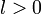 , байтовой строки , байтовой строки 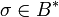 , для которой , для которой 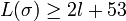 , ,
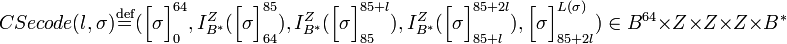 . .
Процесс генерирования подписи
Алгоритм. Генерирование цифровой подписи ACE.
Вход: открытый ключ 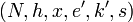 и соответствующий закрытый ключ и соответствующий закрытый ключ 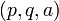 и байтовая строка и байтовая строка 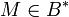 , , 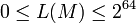 . .
Выход: байтовая строка — цифровая подпись 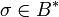 . .
- Произвести следующие действия для хеширования входных данных:
- Сгенерировать случайно ключ хеша
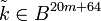 , такой что , такой что 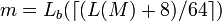 . .
- Вычислить
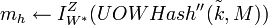 . .
- Выбрать случайное
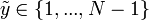 , и вычислить , и вычислить 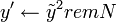 . .
- Вычислить
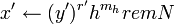 . .
- Сгенерировать случайное простое число
 , , 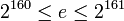 , и его подтверждение корректности , и его подтверждение корректности 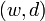 : : 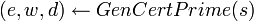 . Повторять этот шаг до тех пор, когда . Повторять этот шаг до тех пор, когда 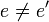 . .
- Положить
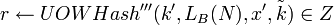 ; заметим, что ; заметим, что 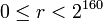 . .
- Вычислить
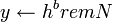 , где , где
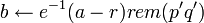 , ,
и где 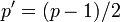 и и 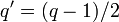 . .
- Закодировать подпись:
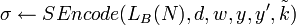 . .
Просмотров: 4051
|
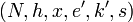 .
.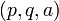 .
.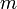 , такого что
, такого что 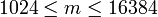 , компоненты ключей определяются следующим образом:
, компоненты ключей определяются следующим образом: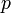 —
— 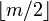 -битное простое число, для которого
-битное простое число, для которого 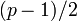 — тоже простое.
— тоже простое.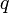 —
— 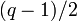 — тоже простое.
— тоже простое.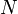 —
— 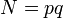 и может иметь как
и может иметь как 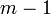 бит.
бит.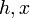 — элементы
— элементы 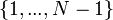 .
.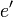 — 161-битное простое число.
— 161-битное простое число.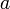 — элемент
— элемент 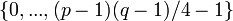
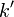 — элементы
— элементы 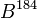 .
. — элементы
— элементы 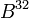 .
.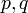 , такие что
, такие что 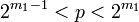 ,
, 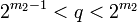 , и
, и 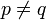 ,
,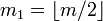 и
и 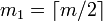 .
.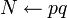 .
.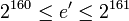 .
.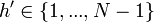 , при условии
, при условии 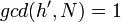 и
и 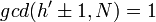 , и вычислить
, и вычислить 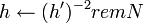 .
.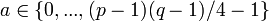 и вычислить
и вычислить 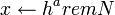 .
.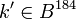 , и
, и 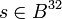 .
.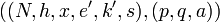 .
.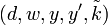 , где компоненты определяются следующим образом:
, где компоненты определяются следующим образом: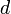 — элемент
— элемент 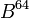 .
.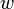 — целое число, такое что
— целое число, такое что 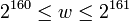 .
.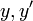 — элементы
— элементы 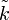 — элемент
— элемент 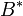 ;заметим, что
;заметим, что 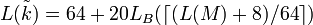 , где
, где 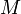 — подписываемое сообщение.
— подписываемое сообщение.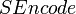 , которая представляет подпись в виде байтовой строки, а также обратную функцию
, которая представляет подпись в виде байтовой строки, а также обратную функцию 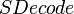 . Для целого
. Для целого 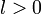 , байтовой строки
, байтовой строки 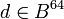 , целых
, целых 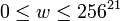 и
и 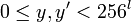 , и байтовой строки
, и байтовой строки 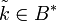 ,
,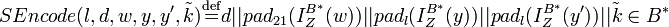 .
.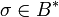 , для которой
, для которой 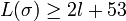 ,
,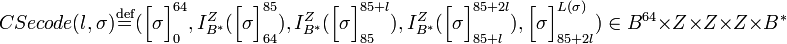 .
.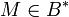 ,
, 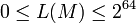 .
.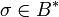 .
.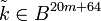 , такой что
, такой что 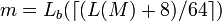 .
.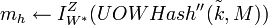 .
.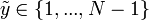 , и вычислить
, и вычислить 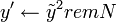 .
.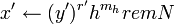 .
. ,
, 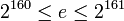 , и его подтверждение корректности
, и его подтверждение корректности 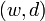 :
: 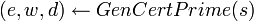 . Повторять этот шаг до тех пор, когда
. Повторять этот шаг до тех пор, когда 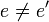 .
.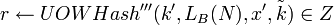 ; заметим, что
; заметим, что 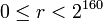 .
.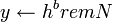 , где
, где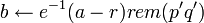 ,
,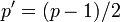 и
и 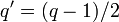 .
.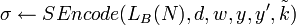 .
.