|
|
|
Компьютеры - ACE Encrypt - Схема шифрования30 апреля 2011
Оглавление:
1. ACE Encrypt
2. Безопасность
3. Схема шифрования
4. Схема цифровой подписи
5. Замечания
Пара ключей шифрования
В схеме шифрования ACE задействованы два типа ключей:
открытый ключ ACE: 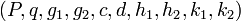 . .
закрытый ключ ACE: 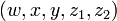 . .
Для заданного параметра размера 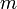 , такого что , такого что 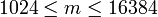 , компоненты ключей определяются следующим образом: , компоненты ключей определяются следующим образом:
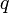 — 256-битное простое число. — 256-битное простое число.
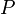 — m-битное простое число, такое что — m-битное простое число, такое что 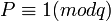 . .
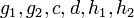 — элементы — элементы 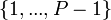 . .
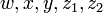 — элементы — элементы  . .
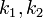 — элементы — элементы 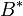 , для которых , для которых 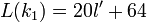 и и 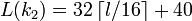 , где , где 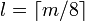 и и 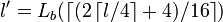 . .
Генерация ключа
Алгоритм. Генерация ключа для схемы шифрования ACE.
Вход: параметра размера 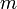 , такой что , такой что 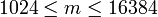 . .
Выход: пара открытый/закрытый ключ.
- Сгенерировать случайное простое число
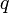 , такое что , такое что 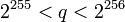 . .
- Сгенерировать случайное простое число
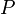 , , 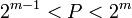 , такое что , такое что 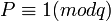 . .
- Сгенерировать случайное целое число
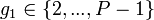 , такое что , такое что 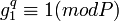 . .
- Сгенерировать случайные целые числа
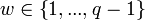 и и 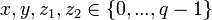
- Вычислить следующие целые числа в
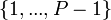 : :
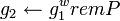 , ,
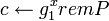 , ,
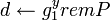 , ,
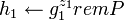 , ,
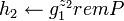 . .
- Сгенерировать случайные байтовые строки
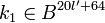 и и 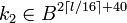 , где , где 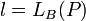 и и 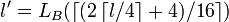 . .
- Вернуть пару открытый/закрытый ключ
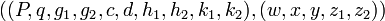
Представление шифротекста
Шифротекст в схеме шифрования ACE имеет вид
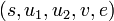 , ,
где компоненты определяются следующим образом:
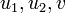 — целые числа из — целые числа из 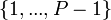 . .
 — элемент — элемент 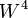 . .
 — элемент — элемент 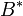 . .
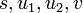 назовём преамбулой, а назовём преамбулой, а  — криптограммой. Если текст — строка из — криптограммой. Если текст — строка из 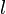 байт, то тогда длина байт, то тогда длина  равна равна 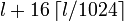 . .
Необходимо ввести функцию 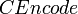 , которая представляет шифротекст в виде байтовой строки, а также обратную функцию , которая представляет шифротекст в виде байтовой строки, а также обратную функцию 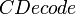 . Для целого . Для целого 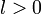 , символьной строки , символьной строки 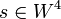 , целых , целых 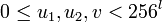 , и байтовой строки , и байтовой строки 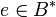 , ,
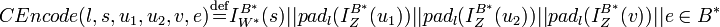 . .
Для целого 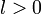 , байтовой строки , байтовой строки 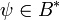 , для которой , для которой 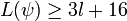 , ,
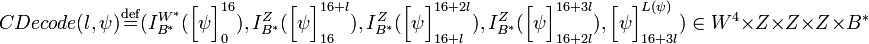 . .
Процесс шифрования
Алгоритм. Ассимметричный процесс шифрования ACE.
Вход: открытый ключ 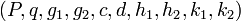 и байтовая строка и байтовая строка 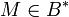 . .
Выход: байтовая строка — шифротекст 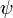 , полученный из , полученный из 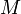 . .
- Сгенерировать случайное
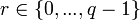 . .
- Сгенерировать преамбулу шифротекста:
- Сгенерировать
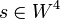 . .
- Вычислить
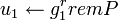 , , 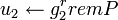 . .
- Вычислить
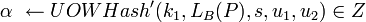 ; заметим, что ; заметим, что 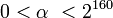 . .
- Вычислить
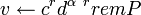 . .
- Вычислить ключ для операции симметричного шифрования:
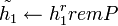 , , 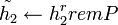 . .- Вычислить
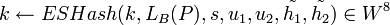 . .
- Вычислить криптограмму
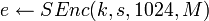 . .
- Закодировать шифротекст:
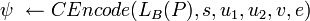 . .
- Вернуть
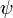 . .
Перед запуском процесса симметричного шифрования входное сообщение 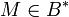 разбивается на блоки разбивается на блоки 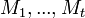 , где каждый блок кроме, возможно, последнего имеет 1024 байт. Каждый блок шифруется потоковым шифратором. Для каждого зашифрованного блока , где каждый блок кроме, возможно, последнего имеет 1024 байт. Каждый блок шифруется потоковым шифратором. Для каждого зашифрованного блока 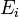 вычисляется 16-байтовый код аутентификации. Получаем криптограмму вычисляется 16-байтовый код аутентификации. Получаем криптограмму
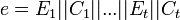 . .
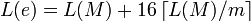 . Заметим, что если . Заметим, что если 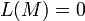 , то , то 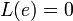 . .
Алгоритм. Симметричный процесс шифрования ACE.
Вход: 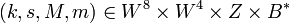 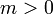
Выход: 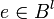 , , 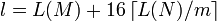 . .
- Если
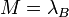 , тогда вернуть , тогда вернуть 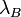 . .
- Проинициализировать генератор псевдо-случайных чисел:
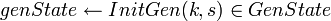
- Сгенерировать ключ
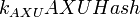 : :
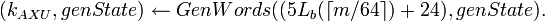 . .
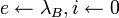 . .- Пока
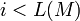 , выполнять следующее: , выполнять следующее:
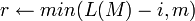 . .- Сгенерировать значения масок для шифрования и MAC:
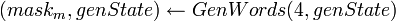 . .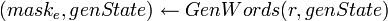 . .
- Зашифровать текст:
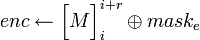 . .
- Сгенерировать аутентификационный код сообщения:
- Если
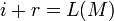 , тогда , тогда 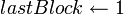 ; иначе ; иначе 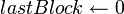 . .
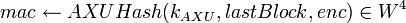 . .
- Обновить шифротекст:
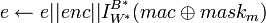 . .
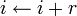 . .
- Вернуть
 . .
Процесс дешифрования
Алгоритм. Процесс дешифрования ACE.
Вход: открытый ключ 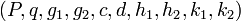 и соответствующий закрытый ключ и соответствующий закрытый ключ 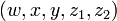 , байтовая строка , байтовая строка 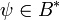 . .
Выход: Расшифрованное сообщение 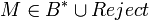 . .
- Дешифровать шифротекст:
- Если
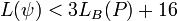 , тогда вернуть , тогда вернуть 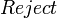 . .
- Вычислить:
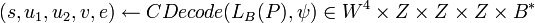 ; ;
заметим, что 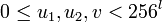 , где , где 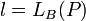 . .
- Подтвердить преамбулу шифротекста:
- Если
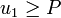 или или 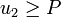 или или 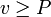 , тогда вернуть , тогда вернуть 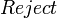 . .
- Если
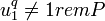 , тогда вернуть , тогда вернуть 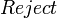 . .
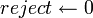 . .- Если
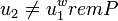 , тогда , тогда 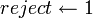 . .
- Вычислить
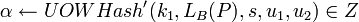 ; заметим, что ; заметим, что 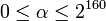 . .
- Если
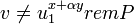 , тогда , тогда 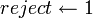 . .
- Если
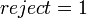 , тогда вернуть , тогда вернуть 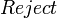 . .
- Вычислить ключ для процесс симметричного дешифрования:
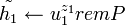 , , 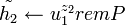 . .- Вычислить
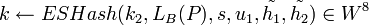 . .
- Вычислить
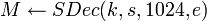 ;заметим, что ;заметим, что 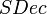 может вернуть может вернуть 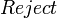 . .
- Вернуть
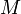 . .
Алгоритм. Операция дешифрования 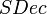 . .
Вход: 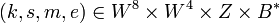 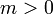
Выход: Расшифрованное сообщение 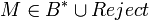 . .
- Если
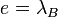 , тогда вернуть , тогда вернуть 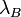 . .
- Проинициализировать генератор псевдо-случайных чисел:
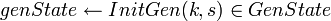
- Сгенерировать ключ
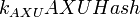 : :
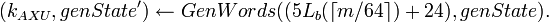 . .
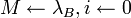 . .- Пока
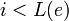 , выполнять следующее: , выполнять следующее:
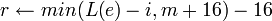 . .- Если
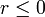 , тогда вернуть , тогда вернуть 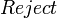 . .
- Сгенерировать значения масок для шифрования и MAC:
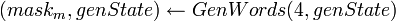 . .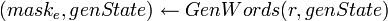 . .
- Подтвердить аутентификационный код сообщения:
- Если
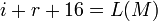 , тогда , тогда 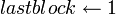 ; иначе ; иначе 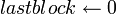 . .
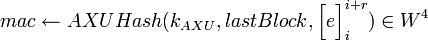 . .- Если
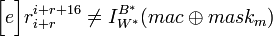 , тогда вернуть , тогда вернуть 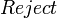 . .
- Обновить текст:
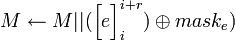 . .
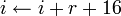 . .
- Вернуть
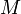 . .
Просмотров: 4058
|
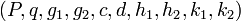 .
.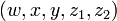 .
.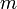 , такого что
, такого что 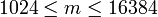 , компоненты ключей определяются следующим образом:
, компоненты ключей определяются следующим образом: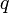 — 256-битное простое число.
— 256-битное простое число.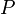 — m-битное простое число, такое что
— m-битное простое число, такое что 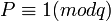 .
.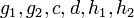 — элементы
— элементы 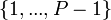 .
.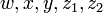 — элементы
— элементы  .
.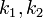 — элементы
— элементы 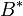 , для которых
, для которых 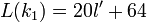 и
и 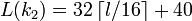 , где
, где 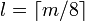 и
и 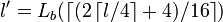 .
.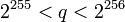 .
.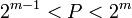 , такое что
, такое что 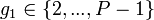 , такое что
, такое что 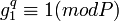 .
.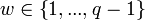 и
и 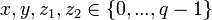
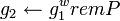 ,
,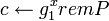 ,
,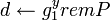 ,
,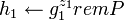 ,
,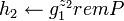 .
.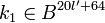 и
и 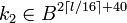 , где
, где 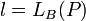 и
и 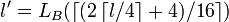 .
.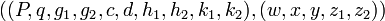
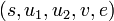 ,
,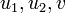 — целые числа из
— целые числа из  — элемент
— элемент 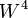 .
. — элемент
— элемент 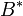 .
.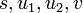 назовём преамбулой, а
назовём преамбулой, а 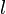 байт, то тогда длина
байт, то тогда длина 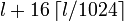 .
.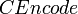 , которая представляет шифротекст в виде байтовой строки, а также обратную функцию
, которая представляет шифротекст в виде байтовой строки, а также обратную функцию 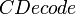 . Для целого
. Для целого 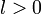 , символьной строки
, символьной строки 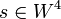 , целых
, целых 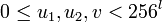 , и байтовой строки
, и байтовой строки 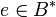 ,
,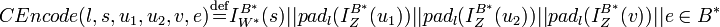 .
.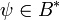 , для которой
, для которой 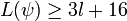 ,
,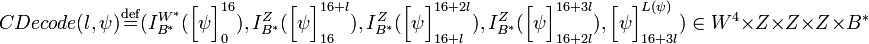 .
.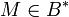 .
.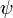 , полученный из
, полученный из 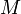 .
.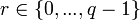 .
.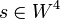 .
.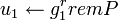 ,
, 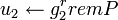 .
.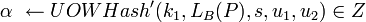 ; заметим, что
; заметим, что 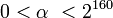 .
.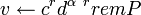 .
.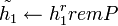 ,
, 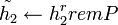 .
.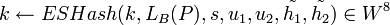 .
.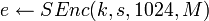 .
.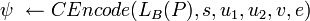 .
.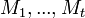 , где каждый блок кроме, возможно, последнего имеет 1024 байт. Каждый блок шифруется потоковым шифратором. Для каждого зашифрованного блока
, где каждый блок кроме, возможно, последнего имеет 1024 байт. Каждый блок шифруется потоковым шифратором. Для каждого зашифрованного блока 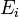 вычисляется 16-байтовый код аутентификации. Получаем криптограмму
вычисляется 16-байтовый код аутентификации. Получаем криптограмму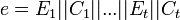 .
.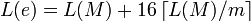 . Заметим, что если
. Заметим, что если 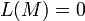 , то
, то 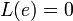 .
.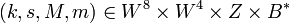
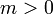
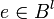 ,
, 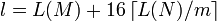 .
.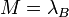 , тогда вернуть
, тогда вернуть 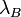 .
.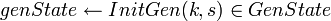
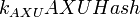 :
: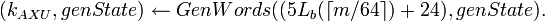 .
.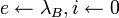 .
.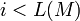 , выполнять следующее:
, выполнять следующее:
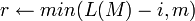 .
.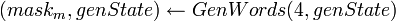 .
.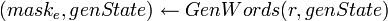 .
.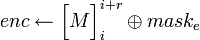 .
.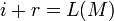 , тогда
, тогда 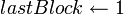 ; иначе
; иначе 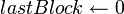 .
.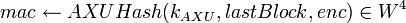 .
.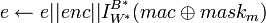 .
.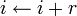 .
.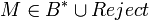 .
.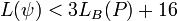 , тогда вернуть
, тогда вернуть 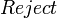 .
.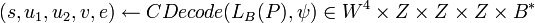 ;
;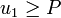 или
или 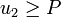 или
или 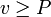 , тогда вернуть
, тогда вернуть 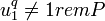 , тогда вернуть
, тогда вернуть 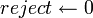 .
.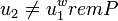 , тогда
, тогда 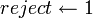 .
.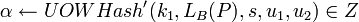 ; заметим, что
; заметим, что 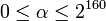 .
.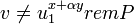 , тогда
, тогда 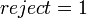 , тогда вернуть
, тогда вернуть 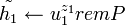 ,
, 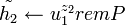 .
.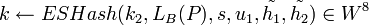 .
.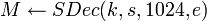 ;заметим, что
;заметим, что 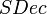 может вернуть
может вернуть 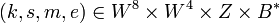
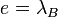 , тогда вернуть
, тогда вернуть 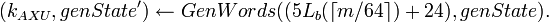 .
.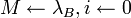 .
.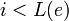 , выполнять следующее:
, выполнять следующее:
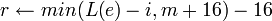 .
.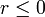 , тогда вернуть
, тогда вернуть 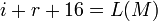 , тогда
, тогда 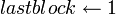 ; иначе
; иначе 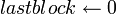 .
.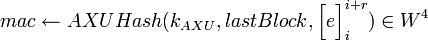 .
.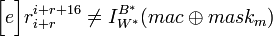 , тогда вернуть
, тогда вернуть 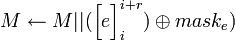 .
.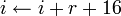 .
.