Компьютеры - ACE Encrypt - Безопасность30 апреля 2011
Оглавление:
1. ACE Encrypt
2. Безопасность
3. Схема шифрования
4. Схема цифровой подписи
5. Замечания
Доказательство безопасности схемы шифрования и схемы цифровой подписи в ACE проводится с использованием обоснованных и естественных допущений. Четырьмя основными допущениями являются:
- Допущение Диффи-Хеллмана
- Сильное допущение RSA
- Стойкость к коллизиям на второй прообраз в SHA-1
- Псевдо-случайность режима сумматора/счетчика MARS
Основные обозначения и терминология
Приведем определения некоторых обозначений и терминов, используемых в данной статье.
Основные математические обозначения
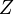 — множество целых чисел. — множество целых чисел.
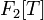 — множество одномерных полиномов с коэффициентами в конечном поле — множество одномерных полиномов с коэффициентами в конечном поле 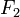 с числом элементов поля — 2. с числом элементов поля — 2.
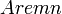 — такое целое число — такое целое число 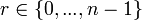 , для которого , для которого 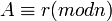 при целом при целом 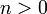 и и 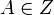 . .
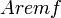 — такой полином — такой полином 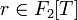 с с 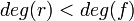 , такой что , такой что 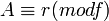 при при 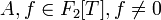 . .
Основные строковые обозначения
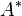 — множество всевозможных строк. — множество всевозможных строк.
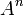 — множество всевозможных строк длины n. — множество всевозможных строк длины n.
Для 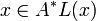 — длина строки — длина строки 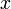 . Обозначения для длины нулевой строки — . Обозначения для длины нулевой строки — 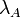 . .
Для 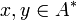 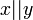 — результат конкатенации строк — результат конкатенации строк 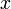 и и 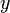 . .
Биты, байты, слова
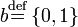 — множество битов. — множество битов.
Рассмотрим множества вида 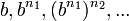 . Для такого множества A определим нулевой элемент: . Для такого множества A определим нулевой элемент:
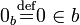 ; ;
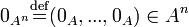 для для 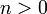 . .
Определим 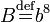 как множество байтов, а как множество байтов, а 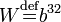 как множество слов. как множество слов.
Для 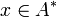 с с 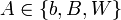 и и 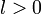 определим оператор заполнения: определим оператор заполнения:
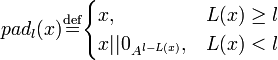 . .
Оператор преобразования
Оператор преобразования 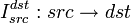 выполняет преобразования между элементами выполняет преобразования между элементами 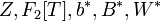 . .
Просмотров: 4052
|
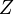 — множество целых чисел.
— множество целых чисел.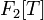 — множество одномерных полиномов с коэффициентами в конечном поле
— множество одномерных полиномов с коэффициентами в конечном поле 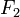 с числом элементов поля — 2.
с числом элементов поля — 2.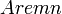 — такое целое число
— такое целое число 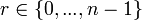 , для которого
, для которого 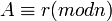 при целом
при целом 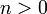 и
и 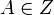 .
.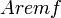 — такой полином
— такой полином 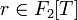 с
с 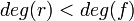 , такой что
, такой что 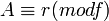 при
при 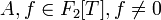 .
.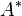 — множество всевозможных строк.
— множество всевозможных строк.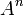 — множество всевозможных строк длины n.
— множество всевозможных строк длины n.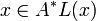 — длина строки
— длина строки 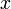 . Обозначения для длины нулевой строки —
. Обозначения для длины нулевой строки — 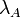 .
.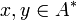
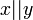 — результат конкатенации строк
— результат конкатенации строк 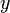 .
.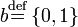 — множество битов.
— множество битов.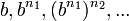 . Для такого множества A определим нулевой элемент:
. Для такого множества A определим нулевой элемент: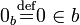 ;
;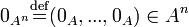 для
для 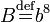 как множество байтов, а
как множество байтов, а 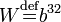 как множество слов.
как множество слов.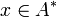 с
с 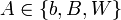 и
и 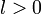 определим оператор заполнения:
определим оператор заполнения: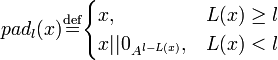 .
.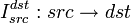 выполняет преобразования между элементами
выполняет преобразования между элементами 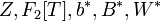 .
.