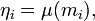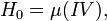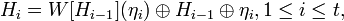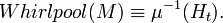Интернет магазин китайских планшетных компьютеров |
||||||||||||||||
Компьютеры - Whirlpool (криптография) - Описание30 марта 2011Оглавление: 1. Whirlpool (криптография) 2. Описание 3. Криптостойкость 4. Применение ВведениеВ данной статье описывается последняя версия Whirlpool. В отличие от первой версии S-box определен, а диффузная матрица заменена на новую после доклада Taizo Shirai и Kyoji Shibutani . Whirlpool состоит из повторного применения функции сжатия , основой которой является специальный 512-битный блочный шифр W с 512-битным ключом. Используемые обозначения и операцииВ алгоритме используются операции в поле Галуа Многочлены для краткости записываются в шестнадцатеричном представлении. Например, запись
Формат данныхКак уже говорилось выше, Whirlpool построена на специальном блочном шифре W, который работает с 512-битными данными. В преобразованиях промежуточный результат вычисления хеша называется хеш-состоянием или просто состоянием. При вычислениях состояние обычно представляется матрицей состояния. Для Whirlpool это матрица в Проще говоря, заполнение матрицы состояния данными происходит построчно. При этом каждый байт матрицы представляет собой соответствующий многочлен в ПреобразованияНелинейное преобразование γФункция Блок подстановки описывается следующей таблицей замен:
Циклическая перестановка πПерестановка Задача данного преобразования — перемешать байты строк матрицы состояния между собой. Линейная диффузия θЛинейная диффузия
Другими словами, матрица состояния умножается справа на матрицу
Как уже упоминалось выше, MDS матрица в последней версии Whirlpool была изменена благодаря статье Taizo Shirai и Kyoji Shibutani . Они проанализировали MDS матрицу второй версии Whirlpool и указали на возможность повышения устойчивости Whirlpool к дифференциальному криптоанализу. Также они предложили 224 кандидата на место новой MDS матрицы . Из этого списка авторы Whirlpool выбрали вариант, наиболее легко реализуемый в аппаратном обеспечении. Добавление ключа σФункция добавления ключа Константы раунда cВ каждом раунде Отсюда видно, что первая строка матрицы c является результатом применения блока подстановки S к байтовым числам Остальные 7 строк — нулевые. Функция раунда ρДля каждого раунда Расширение ключаДля каждого раунда Таким образом, из известного ключа K производится необходимая последовательность K,...,K ключей для каждого раунда блочного шифра W. Блочный шифр WСпециальный 512-битный блочный шифр где ключи K,...,K порождены описанной выше процедурой расширения ключа. В хеш-функции Whirlpool число раундов R = 10. Дополнение входного сообщенияWhirlpool, как и любая другая хеш-функция, должна осуществлять хеширование сообщения произвольной длины. Поскольку внутренний блок шифрования W работает с 512-битными входными сообщениями, то исходное сообщение необходимо разбить на блоки по 512 бит. При этом последний блок, который содержит конец сообщения, может оказаться не полным. Для решения данной задачи Whirlpool использует алгоритм Меркле-Дамгаарда дополнения входного сообщения. Результатом дополнения сообщения M является сообщение M', длина которого кратна 512. Пусть L — длина исходного сообщения. Тогда M' получается в несколько шагов:
Дополненное сообщение M' записывается в виде и разбивается на 512-битные блоки для дальнейшей обработки. Функция сжатия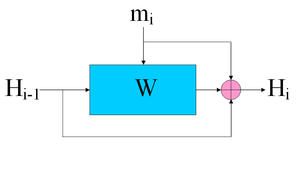
Функция сжатия Whirlpool
В Whirlpool применяется схема хеширования Miyaguchi-Preneel .
где IV) — 512-битная строка, заполненная "0". Вычисление хешаДайджестом для сообщения M является выходное значение Ht функции сжатия, преобразованное обратно в 512-битную строку: Просмотров: 4869
|
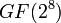 по модулю неприводимого многочлена
по модулю неприводимого многочлена 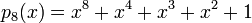 .
.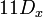 означает
означает 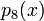 .
. обозначается оператор композиции . Выражение
обозначается оператор композиции . Выражение 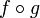 означает композицию функций
означает композицию функций 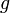 и
и 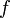 .
.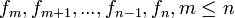 используется символ
используется символ 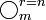 :
: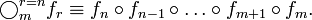
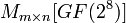 — множество матриц
— множество матриц 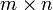 над
над 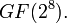
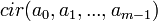 — циркулянтная матрица
— циркулянтная матрица 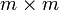 , первая строка которой состоит из элементов
, первая строка которой состоит из элементов 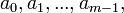 то есть:
то есть: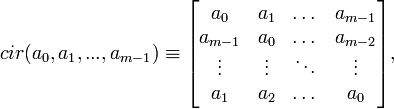
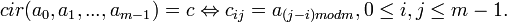
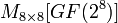 . Следовательно, 512-битные блоки данных должны быть преобразованы в этот формат перед дальнейшими вычислениями. Это достигается введением функции
. Следовательно, 512-битные блоки данных должны быть преобразованы в этот формат перед дальнейшими вычислениями. Это достигается введением функции 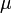 :
: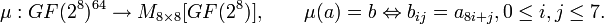
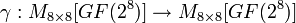 состоит из параллельного применения блока подстановки)
состоит из параллельного применения блока подстановки) 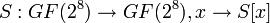 ко всем байтам матрицы состояния:
ко всем байтам матрицы состояния: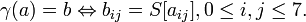
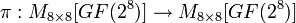 циклически сдвигает каждый столбец матрицы состояния так, что столбец j сдвигается вниз на j позиций:
циклически сдвигает каждый столбец матрицы состояния так, что столбец j сдвигается вниз на j позиций: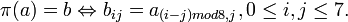
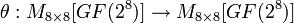 — это линейное преобразование, матрицей которого является MDS матрица
— это линейное преобразование, матрицей которого является MDS матрица 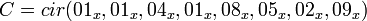 , то есть:
, то есть: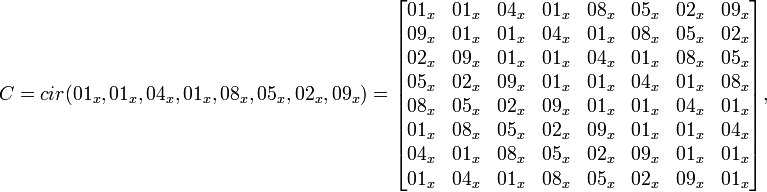
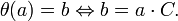
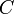 . Напомним, что операции сложения и умножения элементов матриц производятся в
. Напомним, что операции сложения и умножения элементов матриц производятся в 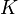 , что если взять её в качестве матрицы линейного преобразования
, что если взять её в качестве матрицы линейного преобразования 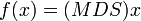 из пространства
из пространства 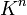 в пространство
в пространство 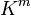 , то любые два вектора из пространства
, то любые два вектора из пространства 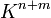 вида
вида 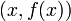 будут иметь как минимум
будут иметь как минимум 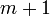 различий в компонентах. То есть набор векторов вида
различий в компонентах. То есть набор векторов вида 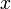 и вектора
и вектора 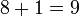 . Другими словами, любое изменение только одного байта
. Другими словами, любое изменение только одного байта 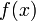 . В этом и состоит задача линейной диффузии .
. В этом и состоит задача линейной диффузии .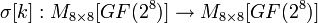 представляет собой побитовое сложение матриц состояния
представляет собой побитовое сложение матриц состояния 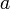 и ключа
и ключа 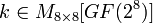 :
: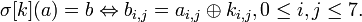
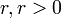 используется матрица констант
используется матрица констант 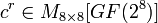 такая, что:
такая, что: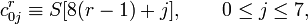

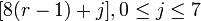 .
. функция раунда — это составное преобразование
функция раунда — это составное преобразование 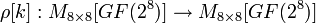 , параметром k которого является матрица ключа
, параметром k которого является матрица ключа 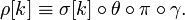
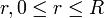 необходим 512-битный ключ шифрования. Для решения данной проблемы во многих алгоритмах вводится так называемая процедура расширения ключа. В Whirlpool расширение ключа реализуется следующим образом:
необходим 512-битный ключ шифрования. Для решения данной проблемы во многих алгоритмах вводится так называемая процедура расширения ключа. В Whirlpool расширение ключа реализуется следующим образом: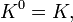
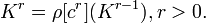
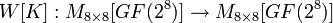 в качестве параметра использует 512-битный ключ K и выполняет следующую последовательность преобразований:
в качестве параметра использует 512-битный ключ K и выполняет следующую последовательность преобразований: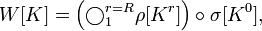
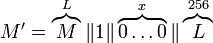
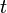 блоков
блоков 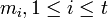 дополненного сообщения M' последовательно шифруются блочным шифром W:
дополненного сообщения M' последовательно шифруются блочным шифром W: