|
|
|
Компьютеры - Троичные функции - Бинарные троичные логические функции23 января 2011
Оглавление:
1. Троичные функции
2. Троичные логические функции
3. Бинарные троичные логические функции
4. Тринарные троичные логические функции
5. N-арные троичные логические функции
Бинарные троичные логические функции
Всего возможно 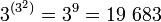 простейших бинарных троичных функций, некоторые из них приведены в таблице: простейших бинарных троичных функций, некоторые из них приведены в таблице:
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
|
|
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
Названия действий |
Обозначения |
|
|
|
|
|
|
|
|
|
|
|
|
| f |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Тождественный ноль |
0 = 0 |
| 0 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
Детектор=2 с 2 при нулях |
|
| 0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
2 |
CGOR |
| 0 |
0 |
0 |
0 |
2 |
2 |
0 |
2 |
1 |
Функция Вебба |
Webb |
| 0 |
0 |
0 |
2 |
0 |
0 |
0 |
2 |
0 |
Детектор=1 с 2 при нулях |
|
| 0 |
0 |
0 |
2 |
0 |
0 |
2 |
2 |
0 |
Детектор x>y с 2 при нулях |
|
| 0 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
Детектор x-y=-2 с 2 при нулях |
|
| 0 |
1 |
0 |
1 |
2 |
1 |
0 |
1 |
0 |
Mean Function Стива Грабба |
x→y |
| 0 |
1 |
2 |
1 |
1 |
2 |
2 |
2 |
2 |
CGAND |
|
| 0 |
2 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
Детектор x-y=-1 с 2 при нулях |
|
| 0 |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
циклический сдвиг вперёд на 1 только одного первого операнда |
СДВИГ1В = СДВИГ1В = SHIFT1F = SHIFTF |
| 0 |
2 |
1 |
2 |
1 |
0 |
1 |
0 |
2 |
Сложение-вычитание в троичной симметричной системе счисления в соответствии
{-1,0,+1}={0,1,2}, sum3s |
|
| 0 |
2 |
2 |
0 |
0 |
2 |
0 |
0 |
0 |
Детектор x<y с 2 при нулях |
|
| 0 |
2 |
2 |
2 |
0 |
2 |
2 |
2 |
0 |
Детектор x≠y с 2 при нулях |
|
| 1 |
0 |
0 |
2 |
1 |
0 |
2 |
2 |
1 |
Magnitude Function Стива Грабба |
|
| 1 |
0 |
2 |
0 |
2 |
1 |
2 |
1 |
0 |
Сложение по модулю 3 в несимметричной системе и в симметричной системе с соответствием {0,1,-1}={0,1,2} или {-1,0,+1}={2,0,1}, summod3ns |
|
| 1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
Разряд переноса при бинарном сложении в несимметричной системе |
carry3n |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Тождественная единица |
1 = 1 |
| 2 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
Разряд переноса при бинарном сложении в троичной симметричной системе счисления с соответствием {0,1,-1}={0,1,2} или {-1,0,+1}={2,0,1} |
carry3s |
| 2 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
2 |
Детектор x=y с 2 при нулях |
|
| 2 |
0 |
0 |
2 |
2 |
0 |
2 |
2 |
2 |
Детектор x>=y с 2 при нулях |
|
| 2 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
Меньшее из двух, минимум, Min Function Стива Грабба |
min=x↓y |
| 2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
повтор только первого аргумента |
ДА1 = YES1 = x |
| 2 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
2 |
Троичная функция следования Брусенцова |
|
| 2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
Разряд переноса при бинарном сложении-вычитании в симметричной троичной системе в соответствии {-1,0,+1}={0,1,2} |
carry3s |
| 2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
повтор только второго аргумента |
ДА2 = YES2 = y |
| 2 |
2 |
2 |
1 |
1 |
2 |
0 |
1 |
2 |
Импликация материальная |
|
| 2 |
2 |
2 |
1 |
2 |
2 |
0 |
0 |
2 |
Импликация Гейтинга |
|
| 2 |
2 |
2 |
1 |
2 |
2 |
0 |
1 |
2 |
Импликация Лукасевича |
|
| 2 |
2 |
2 |
2 |
1 |
1 |
2 |
1 |
0 |
Большее из двух, максимум, Max Function Стива Грабба |
max=x↑y |
| 2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
Тождественная двойка |
2 = 2 |
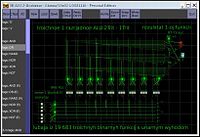
Снимок модели троичного бинарного с унарным выходом АЛУ в трёхбитной одноединичной системе троичных логических элементов в логическом симуляторе Atanua
Все 19 683 простейшие троичные бинарные функции выполняются троичным АЛУ в трёхбитной одноединичной системе троичных логических элементов, снимок модели которого в логическом симуляторе Atanua приведён на рисунке справа.
| x |
1 |
0 |
i |
1 |
0 |
i |
1 |
0 |
i |
|
|
| y |
1 |
1 |
1 |
0 |
0 |
0 |
i |
i |
i |
Названия действий |
Обозначения |
|
|
|
|
|
|
|
|
|
|
|
|
| f |
i |
i |
i |
i |
i |
i |
i |
i |
i |
Тождественный ноль |
0 = 0 |
| i |
i |
i |
i |
1 |
1 |
i |
1 |
0 |
Функция Вебба |
Webb |
| i |
1 |
0 |
i |
1 |
0 |
i |
1 |
0 |
циклический сдвиг вперёд на 1/3 оборота только одного первого операнда |
СДВИГВ = СДВИГВ = SHIFTF = SHIFTF |
| i |
1 |
0 |
1 |
0 |
i |
0 |
i |
1 |
Сложение по модулю 3 в симметричной системе, summod3s |
|
| i |
1 |
1 |
1 |
i |
1 |
1 |
1 |
i |
Детектор x≠y с 2 при нулях |
|
| 0 |
i |
1 |
i |
1 |
0 |
1 |
0 |
i |
Сложение по модулю 3 в несимметричной системе, summod3n |
|
| 0 |
0 |
i |
0 |
i |
i |
i |
i |
i |
Разряд переноса при бинарном сложении в несимметричной системе |
|
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Тождественный ноль |
0 = 0 |
| 1 |
0 |
i |
0 |
0 |
i |
i |
i |
i |
Меньшее из двух, минимум |
min |
| 1 |
0 |
i |
1 |
0 |
i |
1 |
0 |
i |
повтор только первого аргумента |
ДА1 = YES1 = x |
| 1 |
0 |
0 |
0 |
0 |
0 |
i |
0 |
1 |
Троичная функция следования Брусенцова |
|
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
i |
Разряд переноса при бинарном сложении в симметричной троичной системе |
|
| 1 |
1 |
1 |
0 |
0 |
0 |
i |
i |
i |
повтор только второго аргумента |
ДА2 = YES2 = y |
| 1 |
1 |
1 |
0 |
0 |
1 |
i |
0 |
1 |
Импликация материальная |
|
| 1 |
1 |
1 |
0 |
1 |
1 |
i |
i |
1 |
Импликация Гейтинга |
|
| 1 |
1 |
1 |
0 |
1 |
1 |
i |
0 |
1 |
Импликация Лукасевича |
|
| 1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
i |
Большее из двух, максимум |
max |
| 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Тождественная единица |
1 = 1 |
Логическое больше
Результат изменяется при перемене мест операндов.
Истинно=1
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| x>y |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
Истинно=2
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| x>y |
0 |
0 |
0 |
2 |
0 |
0 |
2 |
2 |
0 |
Логическое меньше
Результат изменяется при перемене мест операндов.
Истинно=1
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| x<y |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
Истинно=2
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| x<y |
0 |
2 |
2 |
0 |
0 |
2 |
0 |
0 |
0 |
Логическое равенство в троичной логике Лукасевича
Вычисляется eqv; x eqv y;
Результат не изменяется при перемене мест операндов.
В несимметричной троичной системе счисления:
Истинно=1
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| x=y |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
Истинно=2
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| x=y |
2 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
2 |
или
x
^
|
2 | 0 0 2
1 | 0 2 0
0 | 2 0 0
---+----------> y
| 0 1 2
или в виде тринарной матрицы
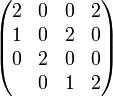
в симметричной троичной системе счисления:
| x |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
| x=y |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
или
x
^
|
1 | 1 1 1
0 | 1 1 1
1 | 1 1 1
---+----------> y
| 1 0 1
Цифровой компаратор
Сравнивает два кода и имеет трёхзначный выход: меньше, равно, больше. Является объединением трёх предыдущих отдельных троичных бинарных функций.
Результат изменяется при перемене мест операндов.
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
1-й операнд |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
2-й операнд |
|
|
|
|
|
|
|
|
|
|
|
| x<y |
0 |
2 |
2 |
0 |
0 |
2 |
0 |
0 |
0 |
|
| x=y |
2 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
2 |
|
| x>y |
0 |
0 |
0 |
2 |
0 |
0 |
2 |
2 |
0 |
|
Минимум
Входит в логику Клини.
Результат не изменяется при перемене мест операндов.
Вычисляется min.
В двоичной логике функции min соответствует конъюнкция: x ∧ y, x И y, 2И.
В троичной несимметричной системе счисления:
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| min |
2 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
или
x
^
|
2 | 0 1 2
1 | 0 1 1
0 | 0 0 0
---+----------> y
| 0 1 2
в троичной симметричной системе счисления:
| x |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
| min |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
или
x
^
|
1 | 1 0 1
0 | 1 0 0
1 | 1 1 1
---+----------> y
| 1 0 1
Максимум
Входит в логику Клини.
Результат не изменяется при перемене мест операндов.
Вычисляется max.
В двоичной логике функции max соответствует дизъюнкция: x ∨ y, x ИЛИ y, 2ИЛИ.
В несимметричной троичной системе счисления:
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| max |
2 |
2 |
2 |
2 |
1 |
1 |
2 |
1 |
0 |
или
x
^
|
2 | 2 2 2
1 | 1 1 2
0 | 0 1 2
---+----------> y
| 0 1 2
или в виде тринарной матрицы
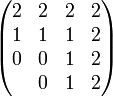
в симметричной троичной системе счисления:
| x |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
| max |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
или
x
^
|
1 | 1 1 1
0 | 0 0 1
1 | 1 0 1
---+----------> y
| 1 0 1
Бинарное сложение в несимметричной троичной системе счисления
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| n+1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
| ⊕3 |
1 |
0 |
2 |
0 |
2 |
1 |
2 |
1 |
0 |
Сложение по модулю 3 в несимметричной троичной системе счисления
Аналог сложения по модулю 2. Название «исключающее ИЛИ», применяемое для «двоичного сложения по модулю 2», для «троичного сложения по модулю 3» неприемлемо, то есть оказалось поверхностным, не глубоким.
Результат не изменяется при перемене мест операндов.
Вычисляется сумма по модулю 3: x ⊕3n y
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| ⊕3n |
1 |
0 |
2 |
0 |
2 |
1 |
2 |
1 |
0 |
или
x
^
|
2 | 2 0 1
1 | 1 2 0
0 | 0 1 2
---+----------> y
| 0 1 2
или в виде тринарной матрицы
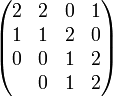
или
⊕3n | 0 1 2
----+----------
0 | 0 1 2
1 | 1 2 0
2 | 2 0 1
или в виде тринарной матрицы
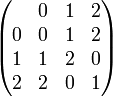
Разряд переноса при бинарном сложении в несимметричной троичной системе счисления
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| n+1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
или в виде тринарной матрицы
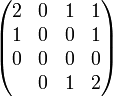
Бинарное сложение в симметричной троичной системе счисления Фибоначчи
| x |
1 |
0 |
i |
1 |
0 |
i |
1 |
0 |
i |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
i |
i |
i |
|
|
|
|
|
|
|
|
|
|
| n+1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
i |
| ⊕3s |
i |
1 |
0 |
1 |
0 |
i |
0 |
i |
1 |
Калька в троичной несимметричной системе счисления:
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| n+1 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
| ⊕3s |
0 |
2 |
1 |
2 |
1 |
0 |
1 |
0 |
2 |
Сложение по модулю 3 в симметричной троичной системе счисления
| x |
1 |
0 |
i |
1 |
0 |
i |
1 |
0 |
i |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
i |
i |
i |
|
|
|
|
|
|
|
|
|
|
| ⊕3s |
i |
1 |
0 |
1 |
0 |
i |
0 |
i |
1 |
x
^
|
1 | 0 1 1
0 | 1 0 1
1 | 1 1 0
--+----------> y
| 1 0 1
или
⊕3s | -1 0 +1
---+----------
-1 | +1 -1 0
0 | -1 0 +1
+1 | 0 +1 -1
Сложение по модулю три напоминает двоичный XOR. Это обычное сложение, только без переноса: в случае переполнения разрядной сетки оно сохраняет лишь младший троичный разряд. Как и двоичный XOR, сложение по модулю три либо оставляет троичный разряд неизменным, либо изменяет его.
Эта функция может быть полезна для реализации троичного полусумматора и сумматора.
Калька в троичной несимметричной системе счисления:
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| ⊕3s |
0 |
2 |
1 |
2 |
1 |
0 |
1 |
0 |
2 |
Разряд переноса при бинарном сложении в симметричной троичной системе счисления
| x |
1 |
0 |
i |
1 |
0 |
i |
1 |
0 |
i |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
i |
i |
i |
|
|
|
|
|
|
|
|
|
|
| n+1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
i |
Калька в троичной несимметричной системе счисления:
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| n+1 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
Импликации
Импликация — логическая связка, соответствующая грамматической конструкции «если …, то …», с помощью которой из двух простых высказываний образуется сложное высказывание. В импликативном высказывании различают антецедент — высказывание, идущее после слова «если», и консеквент — высказывание, идущее за словом «то». Импликативное высказывание представляет в языке логики условное высказывание обычного языка. Последнее играет особую роль как в повседневных, так и в научных рассуждениях, основной его функцией является обоснование одного путём ссылки на нечто другое. В современной логике имеется большое число импликаций, различающихся своими формальными свойствами:
- Троичная функция следования Брусенцова
- импликация материальная
- импликация Гейтинга
- импликация Лукасевича
Троичная функция следования Брусенцова
Вычисляется 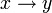 : :
При перемене мест операндов результат изменяется.
в симметричной троичной системе счисления {-1,0,+1}:
| x |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1-е высказывание |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
2-е высказывание |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
следование Брусенцова |
или
x
^
|
1 | 1 0 1
0 | 0 0 0
1 | 1 0 0
---+----------> y
| 1 0 1
в несимметричной троичной системе счисления {0,1,2}:
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
1-е высказывание |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
2-е высказывание |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
2 |
следование Брусенцова |
в несимметричной троичной системе {2,0,1}:
| x |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1-е высказывание |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
2 |
2 |
2 |
2-е высказывание |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
1 |
следование Брусенцова |
Импликация материальная
Материальная импликация — одна из основных связок классической логики. Определяется она таким образом: импликация ложна только в случае истинности основания и ложности следствия, а истинна во всех остальных случаях. Условное высказывание «если x, то y» предполагает некоторую реальную связь между тем, о чём говорится в x и y; выражение «x материально имплицирует y» такой связи не предполагает.
Вычисляется импликация материальная max; 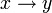 ; x' ∨ y : ; x' ∨ y :
При перемене мест операндов результат изменяется.
в симметричной троичной системе счисления {-1,0,+1}:
| x |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1-е высказывание |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
2-е высказывание |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
Импликация материальная |
или
x
^
|
1 | 1 0 1
0 | 0 0 1
1 | 1 1 1
---+----------> y
| 1 0 1
в несимметричной троичной системе счисления {0,1,2}:
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
1-е высказывание |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
2-е высказывание |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
1 |
1 |
2 |
0 |
1 |
2 |
Импликация материальная |
Импликация Гейтинга
Это часть многозначной логики. Логика Гейтинга охватывала лишь часть классической формальной логики.
Импликацию можно утверждать, только если имеется такое построение, которое, будучи объединено с построением р, автоматически даёт построение q. Например, из истинности высказывания p следует «неверно, что p ложно». Но из утверждения «неверно, что p ложно» ещё не следует, что p — истинно, так как высказывание p может оказаться неконструктивным.
При перемене мест операндов результат изменяется.
В симметричной троичной системе счисления {-1,0,+1}:
x
^
|
1 | 1 0 1
0 | 1 1 1
1 | 1 1 1
---+----------> y
| 1 0 1
| x |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1-е высказывание |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
2-е высказывание |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
Импликация Гейтинга |
В несимметричной троичной системе счисления {0,1,2}:
| x |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
1-е высказывание |
| y |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
2-е высказывание |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
1 |
2 |
2 |
0 |
0 |
2 |
Импликация Гейтинга |
Импликация Лукасевича
Это часть модальной логики.
При перемене мест операндов результат изменяется.
В симметричной троичной системе счисления {-1,0,+1}:
x
^
|
1 | 1 0 1
0 | 0 1 1
1 | 1 1 1
---+----------> y
| 1 0 1
| x |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1-е высказывание |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
2-е высказывание |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
Импликация Лукасевича |
В несимметричной троичной системе счисления {0,1,2}:
| x |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
1-е высказывание |
| y |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
2-е высказывание |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
1 |
2 |
2 |
0 |
1 |
2 |
Импликация Лукасевича |
Логическое сложение по модулю 3 при неполном втором слагаемом
Для сложения одного троичного разряда с разрядом переноса.
Результат не изменяется при перемене мест операндов.
| x |
2 |
1 |
0 |
2 |
1 |
0 |
1-е слагаемое |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
2-е слагаемое |
|
|
|
|
|
|
|
|
|
0 |
2 |
1 |
2 |
1 |
0 |
Сумма по модулю 3 |
или в виде тринарной матрицы
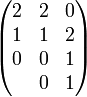
Разряд переноса при сложении с неполным вторым слагаемым
Для сложения одного троичного разряда с разрядом переноса.
Результат не изменяется при перемене мест операндов.
| x |
2 |
1 |
0 |
2 |
1 |
0 |
1-е слагаемое |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
2-е слагаемое |
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
0 |
Перенос в n+1 |
или в виде тринарной матрицы
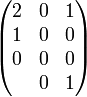
Функция Вебба
Результат не изменяется при перемене мест операндов.
Вычисляется Webb = x | y = ROTF = RotF) = Inc):
в несимметричной троичной системе счисления {0,1,2}:
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
| Webb |
0 |
0 |
0 |
0 |
2 |
2 |
0 |
2 |
1 |
или
x
^
|
2 | 0 0 0
1 | 2 2 0
0 | 1 2 0
---+----------> y
| 0 1 2
или в виде тринарной матрицы
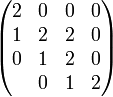
в симметричной троичной системе счисления {-1,0,+1}:
x
^
|
1 | 1 1 1
0 | 1 1 1
1 | 0 1 1
---+----------> y
| 1 0 1
| x |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1-е высказывание |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
2-е высказывание |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
функция Вебба |
Функция Вебба интересна тем, что с помощью неё, подобно штриху Шеффера и стрелке Пирса в двухзначной логике, можно выразить любые трёхзначные функции:
Одноместные:
- RotF = X | X
- RotB = RotF, RotF) = |
- NOT = | RotF | RotF | X))
Двухместные:
- X ∨ Y = RotB.
- X ∧ Y = Not ∨ Not)
Вполне возможно, что именно логическим элементам, реализующим функцию Вебба, придётся сыграть роль троичных ЛА3’их. И от качества реализации этой функции, количества транзисторов будет зависеть эффективность будущих троичных процессоров.
Впрочем, функция ROTB, ROTB) ничем не хуже. Вопрос лишь в том, какую из них мы сможем реализовать наиболее эффективно.
Бинарные функционально полные логические базисы в троичной симметричной системе {-1,0,+1}:
- MAX, СДВИГВ, НЕЛ0, подобно 2ИЛИ-НЕ в двоичной логике
- MAX, СДВИГВ, НЕЛ+1, подобно 2ИЛИ-НЕ в двоичной логике
- MAX, СДВИГВ, НЕЛ-1, подобно 2ИЛИ-НЕ в двоичной логике
- MIN, СДВИГВ, НЕЛ0, подобно 2И-НЕ в двоичной логике
- MIN, СДВИГВ, НЕЛ+1, подобно 2И-НЕ в двоичной логике
- MIN, СДВИГВ, НЕЛ-1, подобно 2И-НЕ в двоичной логике
- MAX, СДВИГН, НЕЛ0, подобно 2ИЛИ-НЕ в двоичной логике
- MAX, СДВИГН, НЕЛ+1, подобно 2ИЛИ-НЕ в двоичной логике
- MAX, СДВИГН, НЕЛ-1, подобно 2ИЛИ-НЕ в двоичной логике
- MIN, СДВИГН, НЕЛ0, подобно 2И-НЕ в двоичной логике
- MIN, СДВИГН, НЕЛ+1, подобно 2И-НЕ в двоичной логике
- MIN, СДВИГН, НЕЛ-1, подобно 2И-НЕ в двоичной логике
Бинарные функционально полные логические базисы в троичных несимметричных системах {2,0,1} и {0,1,2}:
- MAX, СДВИГВ, НЕЛ0, подобно 2ИЛИ-НЕ в двоичной логике
- MAX, СДВИГВ, НЕЛ1, подобно 2ИЛИ-НЕ в двоичной логике
- MAX, СДВИГВ, НЕЛ2, подобно 2ИЛИ-НЕ в двоичной логике
- MIN, СДВИГВ, НЕЛ0, подобно 2И-НЕ в двоичной логике
- MIN, СДВИГВ, НЕЛ1, подобно 2И-НЕ в двоичной логике
- MIN, СДВИГВ, НЕЛ2, подобно 2И-НЕ в двоичной логике
- MAX, СДВИГН, НЕЛ0, подобно 2ИЛИ-НЕ в двоичной логике
- MAX, СДВИГН, НЕЛ1, подобно 2ИЛИ-НЕ в двоичной логике
- MAX, СДВИГН, НЕЛ2, подобно 2ИЛИ-НЕ в двоичной логике
- MIN, СДВИГН, НЕЛ0, подобно 2И-НЕ в двоичной логике
- MIN, СДВИГН, НЕЛ1, подобно 2И-НЕ в двоичной логике
- MIN, СДВИГН, НЕЛ2, подобно 2И-НЕ в двоичной логике
Бинарные троичные логические функции с бинарным выходом
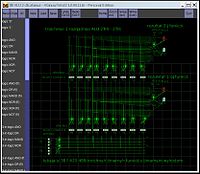
Снимок модели бинарного с бинарным выходом АЛУ в трёхбитной одноединичной системе троичных логических элементов в логическом симуляторе Atanua
Всего возможно 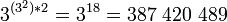 простейших бинарных с бинарным выходом троичных функций. простейших бинарных с бинарным выходом троичных функций.
Все 387 420 489 простейших троичных бинарных с бинарным выходом функций выполняются АЛУ в трёхбитной одноединичной системе троичных логических элементов, приведённым на рисунке справа.
Троичный полусумматор с неполным вторым слагаемым
Первая ступень полного троичного сумматора.
Для сложения одного троичного разряда с разрядом переноса.
Результат не изменяется при перемене мест операндов.
| x |
2 |
1 |
0 |
2 |
1 |
0 |
1-е слагаемое |
| y |
1 |
1 |
1 |
0 |
0 |
0 |
2-е слагаемое |
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
0 |
Перенос в n+1 |
|
0 |
2 |
1 |
2 |
1 |
0 |
Сумма по модулю 3 |
Результат операции занимает 1 и 2/3 троичных разряда.
Троичный полусумматор в несимметричной троичной системе счисления
Троичное логическое сложение двух троичных разрядов с разрядом переноса в несимметричной троичной системе счисления.
Результат не изменяется при перемене мест операндов.
Троичный полусумматор можно рассматривать, как объединение двух бинарных троичных функций: «логического сложения по модулю 3 в троичной несимметричной системе счисления» и «разряд переноса при сложении двух полных троичных разрядов в троичной несимметричной системе счисления».
В отличие от предыдущих бинарных троичных функций с одноразрядным результатом, результат функции занимает 1 и 2/3 троичных разрядов, так как при сложении в троичной несимметричной системе в разряде переноса не бывает значения больше единицы.
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
1-е слагаемое |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
2-е слагаемое |
|
|
|
|
|
|
|
|
|
|
|
| Перенос в n+1, несимметричный |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
| Сумма по модулю 3, несимметричная |
1 |
0 |
2 |
0 |
2 |
1 |
2 |
1 |
0 |
|

Снимок модели троичного полусумматора в несимметричной троичной системе счисления в трёхбитной одноединичной системе логических элементов в логическом симуляторе Atanua.
или в виде матрицы
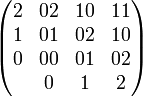
Троичный полусумматор-полувычитатель в симметричной троичной системе счисления
Троичное логическое сложение-вычитание двух троичных разрядов с разрядом переноса в симметричной троичной системе счисления.
Результат не изменяется при перемене мест операндов.
Троичный полусумматор-полувычитатель можно рассматривать, как объединение двух бинарных троичных функций: «логического сложения-вычитания по модулю 3 в троичной симметричной системе счисления» и «разряд переноса при сложении-вычитании двух полных троичных разрядов в троичной симметричной системе счисления».
В отличие от сложения и вычитания в троичной несимметричной системе счисления, результат функции занимает 2 троичных разряда, так как при сложении-вычитании в троичной симметричной системе в разряде переноса бывает двойка.
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
1-е слагаемое-вычитаемое |
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
2-е слагаемое-вычитаемое |
|
|
|
|
|
|
|
|
|
|
|
| Перенос в n+1 разряд, симметричный |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
| Сумма-разность по модулю 3, симметричная |
0 |
2 |
1 |
2 |
1 |
0 |
1 |
0 |
2 |
|
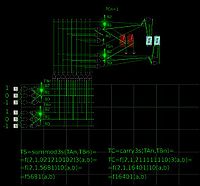
Снимок модели одноразрядного троичного симметричного полусумматора-полувычитателя в трёхбитной системе логических элементов в логическом симуляторе Atanua.
или в виде матрицы
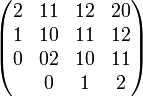
Бинарные троичные логические функции с нонарным результатом
Всего возможно 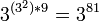 ≈ ≈ 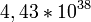 простейших бинарных троичных функций с нонарным результатом. простейших бинарных троичных функций с нонарным результатом.
Троичный дешифратор «2 трита в 9 строк»
Результат изменяется при перемене мест операндов.
Можно рассматривать как объединение девяти бинарных троичных функций с унарными результатами.
| x |
2 |
1 |
0 |
2 |
1 |
0 |
2 |
1 |
0 |
|
| y |
2 |
2 |
2 |
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
| 8 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
| 7 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
| 6 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
| 5 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
| 4 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
| 3 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
| 2 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Бинарные троичные логические функции с m-арными результатами
Всего возможно 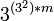 бинарных троичных функций с m-арным выходом, то есть бесконечное число. бинарных троичных функций с m-арным выходом, то есть бесконечное число.
К этим функциям относятся бинарные дешифраторы и демультиплексоры с m-арными выходами.
Просмотров: 9535
|




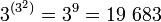 простейших бинарных троичных функций, некоторые из них приведены в таблице:
простейших бинарных троичных функций, некоторые из них приведены в таблице: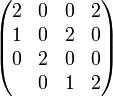
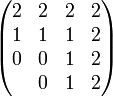
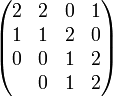
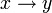 :
:
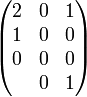
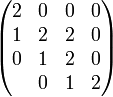
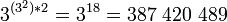 простейших бинарных с бинарным выходом троичных функций.
простейших бинарных с бинарным выходом троичных функций.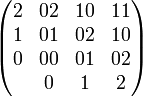
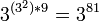 ≈
≈ 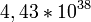 простейших бинарных троичных функций с нонарным результатом.
простейших бинарных троичных функций с нонарным результатом.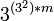 бинарных троичных функций с m-арным выходом, то есть бесконечное число.
бинарных троичных функций с m-арным выходом, то есть бесконечное число.