Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Троичные функции23 января 2011Оглавление: 1. Троичные функции 2. Троичные логические функции 3. Бинарные троичные логические функции 4. Тринарные троичные логические функции 5. N-арные троичные логические функции Троичной функцией в теории функциональных систем и троичной логике называют функцию типа Элементы множества — цифровые знаки 0, 1 и 2 могут интерпретироваться как логические «ложь», «неизвестно» и «истина», в общем случае их смысл может быть любым. Элементы Каждая троичная функция арности n полностью определяется заданием своих значений на своей области определения, то есть на всех троичных векторах длины n. Число таких векторов равно 3. Поскольку на каждом векторе трёхзначная функция может принимать одно из трёх раличных значений, то количество всех n-арных троичных функций равно 3. Например, существует 3 = 3 нульарных троичных логических функций — константы 0, 1 и 2; 3 = 27 унарных троичных логических функций и т. д. Просмотров: 9528
|
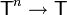 , где
, где 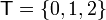 — троичное множество, а
— троичное множество, а 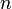 — неотрицательное целое число, которое называют арностью или местностью функции.
— неотрицательное целое число, которое называют арностью или местностью функции.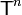 называют троичными векторами. В случае n = 0 троичная функция превращается в троичную константу.
называют троичными векторами. В случае n = 0 троичная функция превращается в троичную константу.