Интернет магазин китайских планшетных компьютеров |
|||||||||||||
Компьютеры - Троичная система счисления - Таблицы сложения в троичных системах счисления22 января 2011Оглавление: 1. Троичная система счисления 2. Таблицы сложения в троичных системах счисления 3. Девятеричная форма представления команд В троичной несимметричной системе счисленияС результатом в десятичной системе счисления:
С результатом в троичной несимметричной системе счисления:
В троичной симметричной системе счисленияС результатом в десятичной системе счисления:
С результатом в троичной симметричной системе счисления:
Симметричная троичная система счисленияПозиционная целочисленная симметричная троичная система счисления была предложена итальянским математиком Фибоначчи для решения «задачи о гирях». Задачу о наилучшей системе гирь рассматривал Лука Пачоли. Частный случай этой задачи был опубликован в книге французского математика Клода Баше де Мезириака «Сборник занимательных задач» в XVII веке в 1612 г. Русский перевод книги К. Г. Баше «Игры и задачи, основанные на математике» вышел в Петербурге в 1877 г. Позже этой задачей занимался петербургский академик Леонард Эйлер, интересовался Д. И. Менделеев. Симметричность при взвешивании на рычажных весах использовали с древнейших времён, добавляя гирю на чашу с товаром. Элементы троичной системы счисления были в системе счисления древних шумеров, в системах мер, весов и денег, в которых были единицы равные 3. Но только в симметричной троичной системе счисления Фибоначчи объединены оба этих свойства. Симметричная система позволяет изображать отрицательные числа, не используя отдельный знак минуса. Число 2 изображается цифрой 1 в разряде троек и цифрой
В соответствии 2. сохраняются числовые значения 0 и 1.
В троичной симметричной системе счисления знак 1 можно заменить знаком i или 2 и, во втором случае, использовать для троичной симметричной системы счисления {-1,0,+1} знаки троичной несимметричной системы {2,0,1}. СвойстваБлагодаря тому что основание 3 нечётно, в троичной системе возможно симметричное относительно нуля расположение цифр: −1, 0, 1, с которым связано пять ценных свойств:
Представление отрицательных чиселНаличие положительной и отрицательной цифр позволяет непосредственно представлять как положительные, так и отрицательные числа. При этом нет необходимости в специальном разряде знака и не надо вводить дополнительный код для выполнения арифметических операций с отрицательными числами. Все действия над числами, представленными в троичной системе счисления с цифрами 0, 1, −1, выполняются естественно с учётом знаков чисел. Знак числа определяется знаком старшей значащей цифры числа: если она положительна, то и число положительно, если отрицательна, то и число отрицательно. Для изменения знака числа надо изменить знаки всех его цифр. Например: ОкруглениеДругим полезным следствием симметричного расположения значений цифр является отсутствие проблемы округления чисел: абсолютная величина части числа, представленной отбрасываемыми младшими цифрами, никогда не превосходит половины абсолютной величины части числа, соответствующей младшей значащей цифре младшего из сохраняемых разрядов. Следовательно, в результате отбрасывания младших цифр числа получается наилучшее при данном количестве оставшихся цифр приближение этого числа, и округление не требуется. Перевод чисел из десятичной системы в троичнуюПеревод чисел из десятичной системы в троичную и соответствующий ему вопрос о гирях подробно изложены в книгах . Там же рассказано о применении троичной системы гирь в русской практике. Перевод в другие системы счисленияВсякое число, записанное в троичной системе счисления с цифрами 0, 1, −1, можно представить в виде суммы целых степеней числа 3, причём если в данном разряде троичного изображения числа стоит цифра 1, то соответствующая этому разряду степень числа 3 входит в сумму со знаком «+», если же цифра −1, то со знаком «-», а если цифра 0, то вовсе не входит. Это можно представить формулой
причём коэффициенты K могут принимать значения { 1, 0, −1 }. Для того чтобы число, представленное в троичной системе, перевести в десятичную систему, надо цифру каждого разряда данного числа умножить на соответствующую этому разряду степень числа 3 и полученные произведения сложить. Практические применения
Просмотров: 24534
|
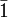 в разряде единиц. Число −2 изображается цифрой
в разряде единиц. Число −2 изображается цифрой 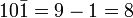
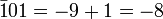
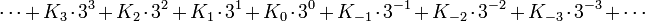 , где
, где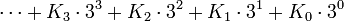 — целая часть числа,
— целая часть числа,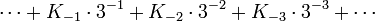 — дробная часть числа,
— дробная часть числа,