Интернет магазин китайских планшетных компьютеров |
|||||||||||
Компьютеры - Троичная система счисления22 января 2011Оглавление: 1. Троичная система счисления 2. Таблицы сложения в троичных системах счисления 3. Девятеричная форма представления команд позиционная система счисления с целочисленным основанием равным 3. Существует в двух вариантах: несимметричная и симметричная. Троичные цифры можно обозначать любыми тремя знаками {A,B,C}, {X,Y,Z}, {!,?,%} и др., но в несимметричной троичной системе счисления чаще применяются цифры {0,1,2}, а в троичной симметричной системе счисления знаки {−,0,+}, {−1,0,+1}, {1,0,1}, {1,0,1}, {i,0,1}, {N,O,P}, {N,Z,P} и цифры {2,0,1}. В цифровой электронике, независимо от варианта троичной системы счисления, одному троичному разряду в троичной системе счисления соответствует один троичный триггер как минимум на трёх инверторах с логикой на входе или два двоичных триггера как минимум на четырёх инверторах с логикой на входе. Представление чисел в троичных системах счисленияНесимметричная троичная система счисленияПримером представления чисел в несимметричной троичной системе счисления может служить запись в этой системе целых положительных чисел:
Если в десятичной системе счисления имеется 10 цифр и веса соседних разрядов различаются в 10 раз, то в троичной системе используются только три цифры и веса соседних разрядов различаются в три раза. Цифра 1, написанная первой левее запятой, обозначает единицу; эта же цифра, написанная второй левее запятой, обозначает тройку и т. д. Несимметричная троичная система счисления является частным случаем спаренных показательных позиционных систем счисления, в которой ak — из троичного множества a={0,1,2}, b=3, веса разрядов равны 3. Сдвоенные комбинированные системы счисленияВ сдвоенных показательных позиционных троичных системах счисления используются две системы счисления:
Целое число в сдвоенной показательной позиционной системе счисления представляется в виде суммы произведений значений в разрядах —
Каждое произведение При b=a образуются -ичные системы счисления с произведением — aka и суммой — Весовой коэффициент разряда — b — приписной и, в общем случае, может быть необязательно показательной функцией от номера разряда — k, и необязательно степенью числа 3. Множество значений ak более ограниченно и более связано с аппаратной частью — числом устойчивых состояний триггеров или числом состояний группы триггеров в одном разряде регистра. В общем случае, ak могут быть тоже необязательно из троичного множества a={0,1,2}, но, чтобы спаренной системе быть троичной и называться троичной, как минимум, одна из двух систем должна быть троичной. Так как ak-тые ближе к аппаратной части и по ak-тым из множества a={0,1,2} или из множества a={-1,0,+1}, а не по b мы определяем и относим число x к троичным системам кодирования, то есть большие основания считать a основным основанием системы счисления, b в таком случае называется основанием вспомогательной системы счисления. Но и это весьма относительно, так как запись числа может быть в одной системе кодирования, а само число может быть в другой системе счисления. Пример: двоично-десятичное кодирование, в котором числа записываются в двоичном коде, а система счисления — десятичная. Сдвоенные комбинированные троичные системы счисленияЦелое число В показательных системах счисления значениям разрядов приписываются весовые коэффициенты b, в записи они опускаются, но подразумевается, что k-тый разряд справа налево имеет весовой коэффициент равный b. Из комбинаторики известно, что число записываемых кодов не зависит от основания показательной функции — b, которое определяет диапазон представляемых числами x3,b величин, и равно числу размещений с повторениями: Дробное число записывается и представляется в виде:
при m=0 дробная часть отсутствует, число — целое, при ak из троичного множества a={0,1,2} и b=1 образуется непозиционная троичная система счисления с одинаковыми весовыми коэффициентами всех разрядов равными 1=1, при ak из двоичного множества a={0,1} и b=3 в сумме будут только целые степени — 3, при ak из троичного множества a={0,1,2} и b=3 в сумме будут целые и удвоенные степени 3, система счисления становится обычной несимметричной троичной системой счисления, ak удовлетворяют неравенству 0<=ak<=<b, т.е. 0<=ak<=2<3, при ak из десятичного множества a={0,1,2,3,4,5,6,7,8,9} и b=3 в сумме будут целые степени 3 умноженные на 1, 2, 3, 4, 5, 6, 7, 8 и 9. Строенные комбинированные троичные системы счисленияВ строенных показательных позиционных троичных системах счисления используются три системы счисления. В вес разряда вводится дополнительный член в третьей системе счисления. Например, сомножитель: В общем случае c≠3. Кодирование троичных цифрОдна троичная цифра может кодироваться разными способами. 2. Двухуровневое двухразрядное двухпроводное кодирование 1: Сравнение с двоичной системой счисленияПри поразрядном сравнении троичная система счисления оказывается более ёмкой, чем двоичная система счисления. СвойстваТроичная позиционная показательная несимметричная система счисления по затратам числа знаков наиболее экономична из позиционных показательных несимметричных систем счисления. А. Кушнеров приписывает эту теорему Джону фон Нейману. Перевод целых чисел из десятичной системы счисления в троичнуюДля перевода целое десятичное число делят нацело с остатком на 3 до тех пор, пока частное больше нуля. Остатки, записанные слева направо от последнего к первому являются целым несимметричным троичным эквивалентом целого десятичного числа. Просмотров: 24540
|
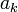 на k-тые степени числа b:
на k-тые степени числа b: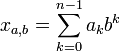 , где:
, где: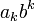 в такой записи называется-ичным разрядом.
в такой записи называется-ичным разрядом.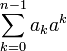 , которые при a=3 превращаются в обычную -ичную систему счисления. При записи первый индекс часто опускается, иногда, когда есть упоминание в тексте, опускается и второй индекс.
, которые при a=3 превращаются в обычную -ичную систему счисления. При записи первый индекс часто опускается, иногда, когда есть упоминание в тексте, опускается и второй индекс.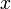 в сдвоенной позиционной троичной системе записывают в виде последовательности его цифр, перечисляемых слева направо по убыванию старшинства разрядов:
в сдвоенной позиционной троичной системе записывают в виде последовательности его цифр, перечисляемых слева направо по убыванию старшинства разрядов: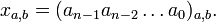
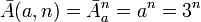 , где:
, где: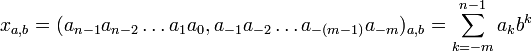 , где m — число разрядов дробной части сдвоенного позиционного числа справа от запятой,
, где m — число разрядов дробной части сдвоенного позиционного числа справа от запятой,