Интернет магазин китайских планшетных компьютеров |
||
Компьютеры - Тестирование псевдослучайных последовательностей23 января 2011Оглавление: 1. Тестирование псевдослучайных последовательностей 2. Графические тесты 3. Статистические тесты 4. Практические приложения совокупность методов определения меры близости заданной псевдослучайной последовательности к случайной. В качестве такой меры обычно выступает наличие равномерного распределения, большого периода, равной частоты появления одинаковых подстрок и т. п. Теоретическая основаПринципы построенияОдин из самых наглядных тестов — тест на равномерное распределение частот появления каждого символа. Пусть ξ1,ξ2...ξn — последовательность длиной n и размерности m. Тогда частоты νi должны принадлежать отрезку Зная вероятностные свойства истинно случайной последовательности, можно на их основе проверять гипотезу о том, насколько сгенерированная последовательность похожа на случайную. Для этого для каждого теста подбирается подходящая статистика, вычисляется её значения для идеальной и сгенерированной последовательности. Если разность этих значений превышает некоторое критическое значение, установленное заранее, то последовательность считается неслучайной. Для «хороших» последовательностей вероятность такого события крайне мала. Однако, существует вероятность того, что «плохая» последовательность удовлетворит критерию и будет сделан вывод о её случайности. На практике значения длины последовательности n, α и β связаны, задаётся α и подбирается n такое, чтобы минимизировать β. Определим величину P-value как вероятность того, что идеальный генератор сгенерировал последовательность менее случайную, чем исследуемый. Тогда если P-value больше α, то исследуемая последовательность считается случайной и наоборот в противном случае. Кратко шаги статистического тестирования можно изобразить в виде таблицы:
Интерпретация результатовПусть дана двоичная последовательность s. Требуется установить проходит ли данная последовательность статистический тест или нет. Разработчиками таких тестов применяются несколько различных подходов в определении этого факта:
Пороговое значениеДанный подход заключается в подсчете какой-либо статистической величины двоичной последовательности с и его сравнении с некоторым пороговым значением. Если полученное значение с меньше порогового значения, то последовательность s не проходит данный тест. Фиксированный диапазон значенийПодход также заключается в подсчете некоторой статистической величины двоичной последовательности с как и в первом случае. Однако теперь мы говорим, что если с выходит за пределы некоторого диапазона значений, то последовательность s не проходит данный тест. Значение вероятностиТретий подход в определении того факта, что двоичная последовательность s проходит статистический тест, включает подсчет не только статистической величины с, но и соответствующее ей значение вероятности p. Обычно подсчет конкретной статистической величины производится таким образом, чтобы её большие значения предполагали неслучайный характер последовательности s. Тогда p есть вероятность получения значения с большего либо равного значению с, высчитанного для истинно случайной последовательности s'. Следовательно, малые значения вероятности p могут быть интерпретированы как доказательство того, что s не является случайной. Таким образом, если для некоторого фиксированного значения a значение вероятности p < a, то двоичная последовательность s не проходит данный тест. Как правило, a принимает значения из интервала. Просмотров: 5068
|
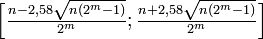 . Однако, большинство тестов используют другой метод — принятие или отклонение гипотезы о случайности последовательности, используя статистические распределения.
. Однако, большинство тестов используют другой метод — принятие или отклонение гипотезы о случайности последовательности, используя статистические распределения.