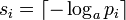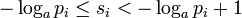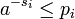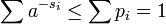Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Теорема Шеннона об источнике шифрования - Доказательство теоремы об источнике шифрования для кодов символов22 января 2011Оглавление: 1. Теорема Шеннона об источнике шифрования 2. Доказательство теоремы об источнике шифрования 3. Доказательство теоремы об источнике шифрования для кодов символов Пусть si длина слова для каждого возможного xi. Определим Тогда где вторая строка является неравенством Гиббса, а пятая строка является неравенством Крафта для второго неравенства мы можем установить и так а затем и таким образом минимальное S удовлетворяет Просмотров: 4088
|
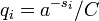 , где С выбирается таким образом, что:
, где С выбирается таким образом, что: 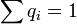 .
.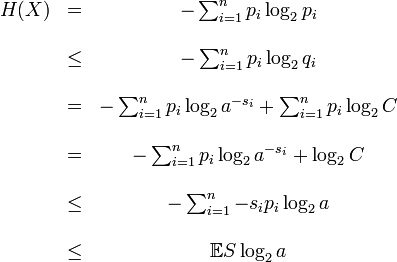
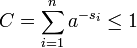
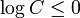 .
.