Интернет магазин китайских планшетных компьютеров |
|
Компьютеры - Теорема Шеннона об источнике шифрования - Доказательство теоремы об источнике шифрования22 января 2011Оглавление: 1. Теорема Шеннона об источнике шифрования 2. Доказательство теоремы об источнике шифрования 3. Доказательство теоремы об источнике шифрования для кодов символов Задано X являющееся НОР, его временной ряд X1, …, Xn также НОР с энтропией H iв случае дискретных значений, и с дифференциальной энтропией в случае непрерывных значений. Теорема об источнике шифрования утверждает что для каждого ε > 0 для каждой оценки большей, чем энтропия ресурса, существует достаточно большое n и шифрователь, который принимает n НОР копий ресурса , X, , и отображает его в n. + ε) двоичных бит таким способом, что исходный символ X может быть восстановлен из двоичных бит, X вероятностью не менее чем 1 − ε. Доказательство Возьмем некоторое ε > 0. формула для,
AEP показывает что для достаточно больших n, последовательность сгенерированная из источника недостоверна в типичном случае — Определение типичных наборов подразумевает, что те последовательности, которые лежат в типичном наборе, удовлетворяют: Заметьте, что:
Начиная с Алгоритм шифрования: шифратор проверяет является ли ложной входящая последовательность, если да, то возвращает индекс входящей частоты в последовательности, если нет, то возвращает случайное n. + ε) digit number. численное значение. В случае если входящая вероятность неверна в последовательности, то шифратор не выдает ошибку. То есть вероятность ошибки составляет выше чем ε Доказательство обратимости Доказательство обратимости базируется на том, что требуется показать что для любой последовательности размером меньше чем Просмотров: 4091
|
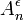 , выглядит следующим образом:
, выглядит следующим образом: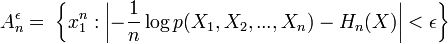
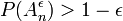
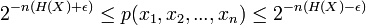
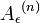 больше чем 1 − ε
больше чем 1 − ε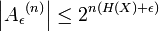 начиная с вероятности полной совокупности
начиная с вероятности полной совокупности 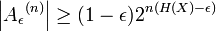 . Fдля доказательства используйте верхнюю границу вероятности для каждого терма в типичном случае, и нижнюю границу для общего случая
. Fдля доказательства используйте верхнюю границу вероятности для каждого терма в типичном случае, и нижнюю границу для общего случая 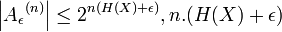 битов достаточно, чтобы отличить любую строку
битов достаточно, чтобы отличить любую строку